I. Introduction
II. A traveler, one map, and two clocks
III. Acceleration and force with one map and two clocks
IV. Problems involving more than one map
V. Conclusions
VI. Acknowledgments
VII. Appendix A: The 4-vector perspective
This appendix provides a more elegant view of matters discussed in the body of this paper by using space-time 4-vectors not used there, along with some promised derivations. We postulate first that: (i) displacements between events in space and time may be described by a displacement 4-vector X for which the time--component may be put into distance-units by multiplying by the speed of light c; (ii) subtracting the sum of squares of space-related components of any 4-vector from the time component squared yields a scalar ``dot-product'' which is frame-invariant, i.e. which has a value which is the same for all inertial observers; and (iii) translational momentum and energy, two physical quantities which are conserved in the absence of external intervention, are components of the momentum-energy 4-vector P = m dX/dtau, where m is the object's rest mass and tau is the frame-invariant displacement in time-units along its trajectory.From above, the 4-vector displacement between two events in space-time is described in terms of the position and time coordinate values for those two events, and can be written as:
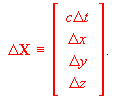 (A1)
(A1)
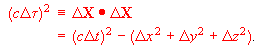 (A2)
(A2)
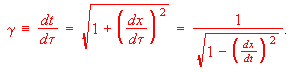 (A3)
(A3)The momentum-energy 4-vector, as mentioned above, is then written using gamma and the components of proper velocity w dx/dtau as:
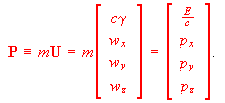 (A4)
(A4)
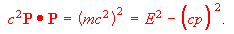 (A5)
(A5)Lastly, the force-power 4-vector may be defined as the proper time derivative of the momentum-energy 4-vector, i.e.:
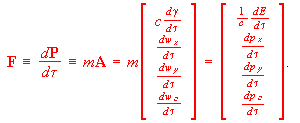 (A6)
(A6)The dot-product of the force-power 4-vector is always negative. It may therefore be used to define the frame-invariant proper acceleration alpha, by writing:
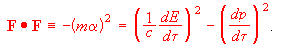 (A7)
(A7)As mentioned in the text, power is classically frame-dependent, but frame-dependence for the components of momentum change only asserts itself at high speed. This is best illustrated by writing out the force 4-vector components for a trajectory with constant proper acceleration, in terms of frame-invariant proper time/acceleration variables tau and alpha. If we consider separately the momentum-change components parallel and perpendicular to the unchanging and frame-independent acceleration 3-vector alpha, one gets
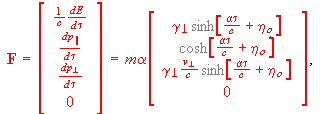 (A8)
(A8)The force responsible for motion, as distinct from the frame-dependent rates of momentum change described above, is that seen by the accelerated object itself. As Eqn. A8 shows for tau, vperp, and etao set to zero, this is nothing more than F = m alpha. Thus some utility for the rapidity/proper time integral of the equations of constant proper acceleration (3rd term in Eqn. 6) is illustrated as well.
VIII. References
IX. Tables
For more on this subject, see our web construction table of contents. Please share your thoughts using our review template, or send comments, answers to problems posed, and/or complaints, to philf@newton.umsl.edu. This page contains original material, so if you choose to echo in your work, in print, or on the web, a citation would be cool.
(Thanks. /philf :)