III. Acceleration and force with one map and two clocks

from ``A one-map two-clock approach to teaching relativity in introductory physics'',
arXiv:physics/9611011 (xxx.lanl.gov archive, Los Alamos, NM, 1996).

Abstract

  • by Phil Fraundorf, Dept. of Physics & Astronomy, University of Missouri-StL
  • Related papers: modernizing Newton, anyspeed modeling, and anticipation.
  • See also: aps1996nov07_001.
  • A copy optimized for printing with Adobe's free Acrobat PDF reader is here.
  • Here are many links on anyspeed motion from a single frame's vantage point.
  • You might also enjoy some of our nanoexploration and information physics links.
  • Symbols: This is a paper has a v-w-u shift in notation from earlier non-coordinate kinematic papers, particularly those which involve the Galilean kinematic.
  • Version release date: 16 Apr 2005.
  • At UM-StLouis see also: a1toc, cme, i-fzx, progs, stei-lab, & wuzzlers.
  • For URL source, cite http://www.umsl.edu/~fraundor/twoclock.html
  • Mindquilts site page requests ~2000/day approaching a million per year.
  • Requests for a "stat-counter linked subset of pages" since 4/7/2005: .

    I. Introduction

    II. A traveler, one map, and two clocks

    III. Acceleration and force with one map and two clocks

    The foregoing relations introduce, in context of a single inertial frame and without Lorentz transforms, many of the kinematical and dynamical relations of special relativity taught in introductory courses, in modern physics courses, and perhaps even in some relativity courses. In this section, we cover less familiar territory, namely the equations of relativistic acceleration. Forces if defined simply as rates of momentum-change in special relativity have no frame-invariant formulation. That is, different map frames will see different forces acting on a given traveler. Moreover, solving problems with coordinate 3-vector acceleration alone can be very messy, indeed {French}.

    Because of this, relativistic acceleration is seldom discussed in introductory courses. Can relativistic equations for constant acceleration, instead, be cast in familiar form? The answer is yes: a frame-invariant 3-vector acceleration, with simple integrals, arises naturally in one-map two-clock relativity. Although the development of the (3+1)D equations is tedious, we show that this acceleration bears a familiar relationship to the frame-independent rate of momentum change (i.e. the force) felt by an accelerated traveler.

    A. Developing the acceleration equations.

    By examining the frame-invariant scalar product of the acceleration 4-vector, one can show (as we do in Appendix A) that a ``proper acceleration'' alpha for our traveler, which is the same to all inertial observers and thus ``frame-invariant'', can be written in terms of components for the classical acceleration vector a by:

    (5)
    This is remarkable, given that a is so strongly frame-dependent! Here the ``transverse time-speed'' gammaperp is defined as 1/Sqrt[1-(vperp/c)^2], where vperp is the component of coordinate-velocity v perpendicular to the direction of coordinate acceleration a. In this section generally, in fact, subscripts || and perp refer to parallel and perpendicular component-directions relative to the direction of this frame-invariant acceleration 3-vector alpha, and not (for example) relative to coordinate velocity v.

    Before considering integrals of the motion for constant proper acceleration alpha, let's review the classical integrals of motion for constant acceleration a. These can be written as a ~ Delta[v||]/Delta[t] ~ (1/2) Delta[v^2]/Delta[x||]. The first of these is associated with conservation of momentum in the absence of acceleration, and the second with the work-energy theorem. These may look more familiar in the form v||f ~ v||i+a Delta[t], and vf^2 ~ vi^2+2a Delta[x||]. Given that coordinate velocity has an upper limit at the speed of light, it is easy to imagine why holding coordinate acceleration constant in relativistic situations requires forces which change even from the traveler's point of view, and is not possible at all for Delta[t] > (c-v||i)/a.

    Provided that proper time tau, proper velocity w, and time-speed gamma can be used as variables, three simple integrals of the proper acceleration can be obtained by a procedure which works for integrating other non-coordinate velocity/time expressions as well {Noncoord}. The resulting integrals are summarized in compact form, like those above, as

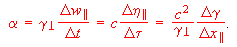    (6)
    Here the integral with respect to proper time tau has been simplified by further defining the hyperbolic velocity angle or rapidity {TaylorWheeler} eta|| = ArcSinh[w||/c] = ArcTanh[v||/c]. Note that both vperp and the ``transverse time-speed'' gammaperp are constants, and hence both proper velocity, and longitudinal momentum p|| = mw||, change at a uniform rate when proper acceleration is held constant. If motion is only in the direction of acceleration, gammaperp is 1, and Delta[p]/Delta[t] = m alpha in the classical tradition.

    In classical kinematics, the rate at which traveler energy E increases with time is frame-dependent, but the rate at which momentum p increases is invariant. In special relativity, these rates (when figured with respect to proper time) relate to each other as time and space components, respectively, of the acceleration 4-vector. Both are frame-dependent at high speed. However, we can define proper force separately as the force felt by an accelerated object. We show in the Appendix that this is simply F = m alpha. That is, all accelerated objects feel a frame-invariant 3-vector force F in the direction of their acceleration. The magnitude of this force can be calculated from any inertial frame, by multiplying the rate of momentum change in the acceleration direction times gammaperp, or by multiplying mass times the proper acceleration alpha. The classical relation F ~ dp/dt ~ m dv/dt = md^2x/dt^2 = ma then becomes:

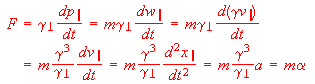    (7)
    Even though the rate of momentum change joins the rate of energy change in becoming frame-dependent at high speed, Newton's 2nd Law for 3-vectors thus retains a frame-invariant form.

    Although they depend on the observer's inertial frame, it is instructive to write out the components of momentum and energy rate-of-change in terms of proper force magnitude F. The classical equation relating rates of momentum change to force is dp/dt ~ F ~ ma i||, where i|| is the unit vector in the direction of acceleration. This becomes

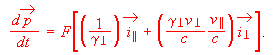    (8)
    Note that if there are non-zero components of velocity in directions both parallel and perpendicular to the direction of acceleration, then momentum changes are seen to have a component perpendicular to the acceleration direction, as well as parallel to it. These transverse momentum changes result because transverse proper velocity wperp = gamma vperp (and hence momentum pperp changes when traveler gamma changes, even though vperp is staying constant.)

    As mentioned above, the rate at which traveler energy increases with time classically depends on traveler velocity through the relation dE/dt ~ Fv|| ~ m (a * v). Relativistically, this becomes

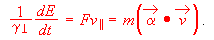    (9)
    Hence the rate of traveler energy increase is in form very similar to that in the classical case.

    Similarly, the classical relationship between work, force, and impulse can be summarized with the relation dE/dx|| ~ F ~ dp||/dt. Relativistically, this becomes

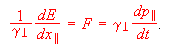    (10)
    Once again, save for some changes in scaling associated with the ``transverse time-speed'' constant gammaperp, the form of the classical relationship between work, force, and impulse is preserved in the relativistic case. Since these simple connections are a result, and not the reason, for our introduction of proper time/velocity in context of a single inertial frame, we suspect that they provide insight into relations that are true both classically and relativistically, and thus are benefits of ``type B'' discussed in the introduction.

    The development above is of course too complicated for an introductory class. However, for the case of unidirectional motion, and constant acceleration from rest, the Newtonian equations have exact relativistic analogs except for the changed functional dependence of kinetic energy on velocity. These equations are summarized in Table II.

    B. Classroom applications of relativistic acceleration and force.

    In order to visualize the relationships defined by Eqn. 6, it is helpful to plot for the (1+1)D or gammaperp=1 case all velocities and times versus x in dimensionless form from a common origin on a single graph (i.e. as v/c, alpha tau/c, w/c=alpha t/c, and gamma versus alpha x/c^2). As shown in Fig. 1, v/c is asymptotic to 1, alpha tau/c is exponential for large arguments, w/c=alpha t/c are hyperbolic, and also tangent to a linear gamma for large arguments. The equations underlying this plot, from Eqn. (6) for gammaperp=1 and coordinates sharing a common origin, can be written simply as:

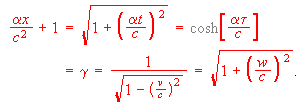    (11)
    This universal acceleration plot, adapted to the relevant range of variables, can be used to illustrate the solution of, and possibly to graphically solve, any constant acceleration problem. Similar plots can be constructed for more complicated trips (e.g. accelerated twin-paradox adventures) and for the (3+1)D case as well {Noncoord}.

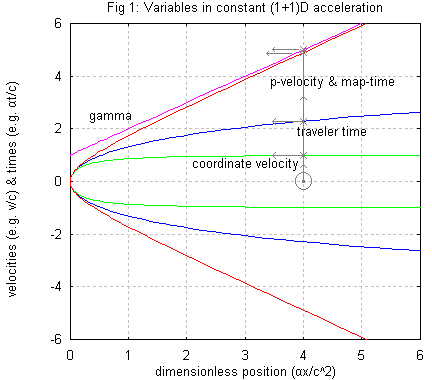
    Figure 1
    Figure 1. The variables involved in (1+1)D constant acceleration.

    With plots of this sort, high school students can solve relativistic acceleration problems with no equations at all! For example, consider constant acceleration from rest at alpha = 1[earth gravity] ~ 1[ly/yr^2] over a distance of 4 [lightyears]. One can read directly from Fig. 1 by drawing a line up from 4 on the x-axis that gamma ~ 5, final proper-speed w ~ 4.8[ly/tyr], map-time t ~ 4.8[yr], proper-time elapsed tau ~ 2.3[tyr], and final coordinate-speed v ~ 1[c]. Problems with most initial value sets can be solved similarly, without equations, on such a plot with help from a straight edge and a bit of trial and error. Of course, the range of variables involved must be reflected in the ranges of the plot. For this reason, it may also prove helpful to replot Fig. 1 on a logarithmic scale. As you can see here, in the classical limit when w << 1[ly/tyr], all variables except gamma (dimensionless times and velocities alike) take on the same value as a function of distance traveled from rest!

    For a numerical example, imagine trying to predict how far one might travel by accelerating at one earth gravity for a fixed traveler-time, and then turning your thrusters around and decelerating for the same traveler-time until you are once more at rest in your starting or ``map'' frame. To be specific, consider the 14.2 proper-year first half of such a trip all the way to the Andromeda galaxy { LagouteDavoust}, one of the most distant (and largest) objects visible to the naked eye. From Eqn. 6, the maximum (final) rapidity is eta|| = alpha tau/c =14.7. Hence the final proper velocity is w = Sinh[alpha tau/c] = 1.2 10^6[ly/tyr]. From Eqn. 2 this means that gamma = Sqrt[1+(w/c)^2] = 1.2 10^6, and the coordinate velocity v = w/Sqrt[1+(w/c)^2] = 0.99999999999963[ly/yr]. Going back to Eqn. 6, this means that coordinate time elapsed is t = w/alpha c = 1.1 10^6[years], and distance traveled x = (gamma -1)c^2/alpha = 1.1 10^6[ly]. Few might imagine, from typical intro-physics treatments of relativity, that one could travel over a million lightyears in less than 15 years on the traveler's clock!

    From Eqn. 5, the coordinate acceleration falls from 1[gee] at the start of the leg to a = alpha/gamma ^3 = 6 10^{-19}[gee] at maximum speed. The forces, energies, and momenta of course depend on the spacecraft's mass. At any given point along the trajectory from the equations above, F is of course just m alpha, dE/dx is gammaperp F = F, dp/dt is F/gammaperp = F, and dE/dt is gammaperp Fv|| = Fv. Note that all except the last of these are constant if mass is constant, albeit dependent on the reference frame chosen. However, the 4-vector components dp/dtau and dE/dtau are not constant at all, showing in another way the pervasive frame-dependences mentioned above.

    The foregoing solution may seem routine, as well it should be. It is not. Note that it was implemented using distances measured (and concepts defined) in context of a single map frame. Moreover, the 3-vector forces and accelerations used and calculated have frame-invariant components, i.e. those particular parameters are correct in context of all inertial frames.

    The mass of the ship in the problem above may vary with time. For example, if the spacecraft is propelled by ejecting particles at velocity u opposite to the acceleration direction, the force felt in the frame of the traveler will be simply m alpha = -udm/dtau. Hence in terms of traveler time the mass obeys m = mo Exp [-alpha tau /u]. In terms of coordinate time, the differential equation becomes m alpha = -u gamma dm/dt. This can be solved to get the solution derived with significantly more trouble in the reference above {LagouteDavoust}.

    IV. Problems involving more than one map

    V. Conclusions

    VI. Acknowledgments

    VII. Appendix A: The 4-vector perspective

    VIII. References

    IX. Tables

    For more, see our web construction table of contents on this subject. Please share your thoughts using our review template, or send comments, answers to problems posed, and/or complaints, to philf@newton.umsl.edu. This page contains original material, so if you choose to echo in your work, in print, or on the web, a citation would be cool. (Thanks. /philf :)