IV. Problems involving more than one map

from ``A one-map two-clock approach to teaching relativity in introductory physics'',
arXiv:physics/9611011 (xxx.lanl.gov archive, Los Alamos, NM, 1996).

Abstract

  • by Phil Fraundorf, Dept. of Physics & Astronomy, University of Missouri-StL
  • Related papers: modernizing Newton, anyspeed modeling, and anticipation.
  • See also: aps1996nov07_001.
  • A copy optimized for printing with Adobe's free Acrobat PDF reader is here.
  • Here are many links on anyspeed motion from a single frame's vantage point.
  • You might also enjoy some of our nanoexploration and information physics links.
  • Symbols: This is a paper has a v-w-u shift in notation from earlier non-coordinate kinematic papers, particularly those which involve the Galilean kinematic.
  • Version release date: 22 Dec 1996.
  • At UM-StLouis see also: a1toc, cme, i-fzx, progs, stei-lab, & wuzzlers.
  • For URL source, cite http://www.umsl.edu/~fraundor/twoclock.html
  • Mindquilts site page requests ~ 2000/day approaching a million per year.
  • Requests for a "stat-counter linked subset of pages" since 4/7/2005: .

    I. Introduction

    II. A traveler, one map, and two clocks

    III. Acceleration and force with one map and two clocks

    IV. Problems involving more than one map

    The foregoing sections treat calculations made possible, and analogies with classical forms which result, if one introduces the proper time/velocity variables in the context of a single map frame. What happens when multiple map-frames are required? In particular, are the Lorentz transform and other multi-map relations similarly simplified or extended? The answer is yes, although our insights in this area are limited since the focus of this paper is introductory physics, and not special relativity.

    A. Development of multi-map equations

    The Lorentz transform itself is simplified with the help of proper velocity, in that it can be written in the symmetric matrix form:

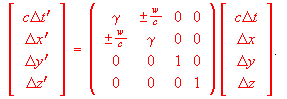    (12)
    This seems to be an improvement over the asymmetric equations normally used, but of course requires a bit of matrix and 4-vector notation that your students may not be ready to exploit.

    The expression for length contraction, namely L = Lo/gamma, is not changed at all. The developments above do suggest that the concept of proper length Lo, as the length of a yardstick in the frame in which it is at rest, may have broader use as well. The relativistic Doppler effect expression, given as f = fo Sqrt[{1+(v/c)}/{1-(v/c)}] in terms of coordinate velocity, also simplifies to f = fo/{gamma -(w/c)}. The classical expression for the Doppler effected frequency of a wave of velocity vwave from a moving source of frequency fo is, for comparison, f = fo/{1-(v/vwave)}.

    The most noticeable effect of proper velocity, on the multi-map relationships considered here, involves simplification and symmetrization of the velocity addition rule. The rule for adding coordinate velocities v' and v to get relative coordinate velocity v'', namely v||'' = (v' + v||)/(1+v||v'/c^2) and vperp'' =/= vperp with subscripts referring to component orientation with respect to the direction of v', is inherently complicated. Moreover, for high speed calculations, the answer is usually uninteresting since large coordinate velocities always add up to something very near to c. By comparison, if one adds proper velocities w' = gamma' v' and w = gamma v to get relative proper velocity w'', one finds simply that the coordinate velocity factors add while the gamma-factors multiply, i.e.

    (13)
    Note that the components transverse to the direction of v' are unchanged. These equations are summarized for the unidirectional motion case in Table III.

    B. Classroom applications involving more than one map-frame.

    Physically more interesting questions can be answered with Eqn. 13 than with the coordinate velocity addition rule commonly given to students. For example, one might ask what the speed record is for relative proper velocity between two objects accelerated by man. For the world record in this particle-based demolition derby, consider colliding two beams from an accelerator able to produce particles of known energy for impact onto a stationary target. From Table I for colliding 50[GeV] electrons in the LEP2 accelerator at CERN, gamma and gamma' are E/mc^2 ~ 50[GeV]/511[keV] ~ 10^5, v and v' are essentially c, and w and w' are hence 10^5[ly/tyr]. Upon collision, Eqn. 13 tells us that the relative proper speed w'' is (10^5)^2(1+1) = 2 10^{10}[ly/tyr]. Investment in a collider thus buys a factor of 2gamma =2 10^5 increase in the momentum (and energy) of collision. Compared to the cost of building a 10[PeV] accelerator for the equivalent effect on a stationary target, the collider is a bargain indeed!

    V. Conclusions

    VI. Acknowledgments

    VII. Appendix A: The 4-vector perspective

    VIII. References

    IX. Tables

    For more on this subject, see our web construction table of contents. Please share your thoughts using our review template, or send comments, answers to problems posed, and/or complaints, to philf@newton.umsl.edu. This page contains original material, so if you choose to echo in your work, in print, or on the web, a citation would be cool. (Thanks. /philf :)