Contents: [Two Tilts] [Fringe Visibility] [Other Stuff]

On-line lattice parameters for any nanocrystal

Most recent developments: Lately our focus has been on ultrahigh temperature materials for use in the aerospace industry, although some of our old naturally-occurring friends (like graphite and SiC from our work on presolar grains formed in the atmosphere of AGB stars and in supernova shocks) are back in new contexts. Because the grains in these ceramics are often microns or larger in size, we've also been adapting our techniques for on-line electron-crystallography to diffraction (where they began early on). Stay tuned for more on that soon as well. On an earlier note, check out the interactive visibility map collection accessible through our Live3D models page. (Note: first select visibilitymaps, and then More Here).

Stereographic fringe-visibility maps for a 3 nm Aluminum nanocrystal in a 300 kV transmission electron microscope able to image lattice spacings down to one Angstrom. These plots were inspired by a T.E.A.M. presentation (here "A" stands for aberration-corrected) in San Antonio (early August 2003) by Wentao. The stereo projection field of these animations covers a full hemisphere (not counting the corners). How would you describe the difference between orientation-space trajectories in the two animations? Hint: Useful concepts might include cube face, edge, corner, face-diagonal, and body-diagonal. If you are into Miller indices, on the other hand, you might talk about "<110> zones" or "{002}-fringe bands". For example, perhaps the trajectory on the left travels around the "waist" of the cubic unit cell, following an (002) band while passing face normal and face diagonal (edge) views in sequence. By comparison the trajectory on the right might go from one ????-diagonal view to the next, rotating at each so as to "follow" the ????? that border a single cubic-cell face. What do you think?

--- Newer animations on our newton server ---
Si{400}8n, Si{220}8n
W{002}8n
Al{200}8n, Al{220}8n
Al{200}3n, Al{220}3n
What do you think that these represent?

Find some "roll your own" band-maps on the University's webMathematica site
starting Oct 2005: fcc_t?A, fcc_80A, fcc_40A, specimen, Fourier color, lattice, atomlist, epcfocus

An application of lattice fringe visibility theory to the study of ordered particle growth on nanocylinders is described in this paper on "Lattice fringe signatures of epitaxy on nanotubes" to cond-mat/0603312.

Fringe visibility theory predicts specific fringe patterns, e.g. for (111) columnar (L) and epitaxial (R) growth.

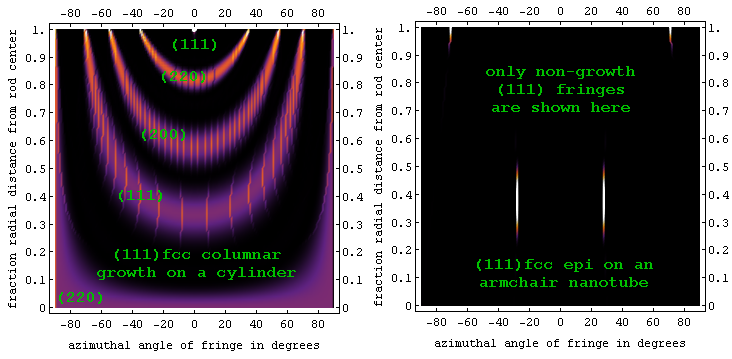
These model predictions are easy (if tedious) to test against angle/position measurements of fringes from individual particles. Digital darkfield techniques provide an alternate way to compare model and experiment.

Making sense of nanocrystal lattice fringes

Sound Bytes: tilt to hide | nano-lattice collimation | now you see it, now you don't

Atom scale tunnels through a crystal become easier and easier to see as the crystal becomes thinner and thinner. This paper examines these effects for crystals in the 2 to 30 nm size range, both experimentally and theoretically working toward rules which allow one to predict quantitatively how crystal size and orientation alter the lattice fringes seen in an electron microscope. The result: Ball-shaped fringe visibility maps that allow one to answer a whole bunch of quantitative questions./pf 2005jan31

Headings: REL spots | lattice fringe visibility | HRTEM | nanocrystal goniometry

Copyright (2005) American Institute of Physics (AIP), this article may be downloaded for personal use only. Any other use requires prior permission of the author and the AIP. It appeared in Journal of Applied Physics 98 (2005) 114308, the Dec 19, 2005 issue of Virtual Journal of Nanoscale Science and Technology, and is more generally available at this URL.

In context of this paper, here are a bunch of online-interactive fringe visibility and Kikuchi maps. Let us know if you find errors, or have other structures you'd like to see mapped.

Here are arXiv PDFs for versions [2] and [1].

Here is updated draft version [2+] , and version [1], both with higher resolution figures.

BiBTeX reference:

@article{wqpf.ncso,
author = "P. Fraundorf, Wentao Qin, P. Moeck, and Eric Mandell",
title = "Making sense of nanocrystal lattice images",
journal = "Journal of Applied Physics",
volume = "98",
year = "2005",
pages = "114308-1--114308-10",
eprint = "arXiv:cond-mat/0212281"}

Clarified version of Figs. 5 and 6 from the MS above, showing the same crystals before and after tilt along with some predictions in the first of these images concerning which fringes will remain visible after tilt (black arrows), and which will not (white arrows)...

Lattice parameters from direct-space images at two tilts

This paper considers how nano-humans might determine the 3D structure of crystals, if they were able to re-orient the crystal in their hand while trying to peer down along tunnels between the columns of atoms which run in various directions. In that case, they could formulate rules (protocols) for everyone to use in recognizing a face-centered cubic crystal, a body-centered cubic crystal, etc. Precisely this type of manipulation (imagine a hand which can only tilt the crystal through a limited angle, over one or two fixed axes) is becoming increasingly possible with modern day atomic resolution transmission electron microscopes. It is therefore time to summarize and refine strategies, including those discussed here./pf 2002oct02

Sound Bytes: hand-analysis for nano-geologists | 3D lattices from images at two tilts | touring crystals on $5/eV

Elsevier's published version is available through ScienceDirect, but posted with permission here only in the Book section of our limited-access Nanoscale Science and Technology Blackboard.

wqpf.lptt PDF draft

BiBTeX reference:

@article{wqpf.lptt,
author = "Wentao Qin and P. Fraundorf",
title = "Lattice parameters from direct-space images at two tilts",
journal = "Ultramicroscopy",
volume = "94",
number = "3-4",
pages = "245--262",
year = "2003",
eprint = "arXiv:cond-mat/0001139"}

Image-Based Crystallography

A subset, and often the whole, reciprocal lattice of a crystal can be inferred from the xyz coordinates of three non-coplanar reciprocal lattice vectors. Such coordinates may be obtained from electron-phase or Z contrast images taken at two tilts, provided that one image shows two non-colinear lattice periodicities, and the other shows a periodicity not coplanar with those two. We show here how to find, and implement, protocols for measuring the 3D parameters of any lattice type in this way. Particularly for cubic crystals with cell side greater than twice the appropriate resolution limit, we show that orthogonal +/-15 and +/-10 degree tilt ranges may allow one to measure 3D parameters of all varieties in a specimen, from only two well-chosen images. The strategy is illustrated by measuring the lattice parameters of a 10nm WC_{1-x} crystal in a plasma-enhanced chemical-vapor-deposited thin film.

Title: On-line determination of nanocrystal lattice parameters
Authors: W. Qin1, 2 and P. Fraundorf1
1Physics/Astronomy Department and Center for Molecular Electronics, University of Missouri-St. Louis, St. Louis, MO 63121
2Process and Materials Characterization Lab, Digital DNATM Labs, Motorola Inc., MD EL622, 2100 E Elliot Road, Tempe, AZ 85284

Selected slides from the summer 2003 presentation

Abstract: The three-dimensional lattice parameters of a selected crystal can be inferred from lattice image information on three sets of non-parallel lattice planes. Today, with sufficiently wide tilt-capability, such data can come from phase-contrast (or less easily Z-contrast) images taken along two low-index zone axes of the crystal (cf. Ultramicroscopy 94, p. 245-262). Higher spatial resolution in images will lessen the requirement for wide-angle tilting, but also increase the geometric complexity of the task due to the involvement of lower symmetry orientations. In addition to some "fancy inverse crystallography" for the design of tilt protocols, our experience so far also suggests that issues of tilt-stage precision, on-line computer support, and off-axis fringe visibility as a function of specimen thickness will have to be considered before routine on-line determination of the lattice parameters of an arbitrary nanocrystal becomes possible in practice.

Other stuff

recent submissions to Microscopy and Microanalysis 2004.

notes by Peter Möck at Portland State on TEM goniometry.

earlier TEAM (aberration-corrected microscopy) presentations.

Papers on fringe visibility maps and lattice parameter uncertainties in PDF form, submitted to MSA 2001.

Wentao's thesis in PDF form.

Papers on tilt (p. 1040-1041) and probability (p. 1038-1039) in PDF form, for MSA 2000.

An early version of a paper on direct-lattice crystallography, archived at Los Alamos in e-print form.

Our first paper on stereo analysis of 2D electron diffraction data.

Above: a fringe-visibility map for 2nm diameter elemental fcc (e.g. Al) crystals (lattice parameter near 0.4nm) in a scope capable of 0.14nm resolution.

Below: Fringe visibility maps for some of the larger fringes visible from body-centered, face-centered, and diamond face-centered lattices. Note the dominance of crossed (110) fringes at the three-fold <111> zone in the body-centered case, the dominant crossed (111) fringes at the two-fold <110> zone in the face-centered cases, and the wider disparity between largest and next-to-largest spacings when the diamond glide is added to the lattice.

A paper in PDF form for the Microscope Society of America Meeting in Summer 1999.

A number of opportunities for wider application, as well as adaptation for on-line use in computer-based microscopes, present themselves downstream...

This page is http://www.umsl.edu/~fraundor/help/imagnxtl.htm. Although there are many contributors, the person responsible for errors is P. Fraundorf. This site is hosted by the Department of Physics and Astronomy (and Center for Molecular Electronics) at UM-StL. Whole-site page requests est. around 2000/day hence more than 500,000/year. Requests for a "stat-counter linked subset of pages" since 4/7/2005: .