Navigation bar: [LAW-ZERO] [cases] [FIRST-LAW] [capacity] [SECOND-LAW] [engines] [LAW-THREE] [surprisal] [evolution] [MORE]
With help from corollaries that scientists were only beginning to explore in the early 20th century, this summary is designed to empower and entice readers with cool connections between introductory physics and mutual information measures applied widely today in: (i) tracking the divergence of evolving codes, (ii) quantum computation, (iii) dynamical study of complex systems, (iv) compressing data, and (v) forensic science including the detection of plagarism.
Note: The concepts used here cut across many technical disciplines. As a result, no attempt is made in traditional physics-exposition style to derive or even to teach the relationships and concepts introduced. References will be provided for those interested in learning more. The objective of this summary, rather, is to alert physics readers to relationships that connect introductory thermal physics concepts to a subset of related developments in other fields.

"Two objects allowed to equilibrate by random sharing with a third object are likewise equilibrated with each other." Random sharing in practice maximizes the collective state-uncertainty Stot = k ln Ω of these two objects, where Ω is the number of accessible states and S is in {nats, bits, or J/K} respectively if k is {1, 1/ln2, or 1.38×10-23}. Individual object uncertainty-slopes converge at this maximum. Hence objects allowed to randomly share...
If the number of accessible states Ω is proportional to EνN/2, this yields equipartition E/N = (ν/2)kT i.e. a prediction that the average thermal energy per degree-of-freedom ν is kT/2 for quadratic systems. If Ω is proportional to VN, the foregoing yields the ideal gas law PV=NkT useful for low-density gases. For systems obeying the law of mass action where Ω is proportional to ζN/N! and ζ is the multiplicity of states accessible to a given molecule, then dS/dN ~ ln[ζ/N]. Thus if a molecule has stoichiometric coefficient b in a reaction, at equilibrium the b-weighted sum of slopes goes to zero and the product of (ζ/N)b for each reactant goes to one. Along with equilibrium values for E, V and N, such analyses also predict the size of fluctuations from one molecule to the next.
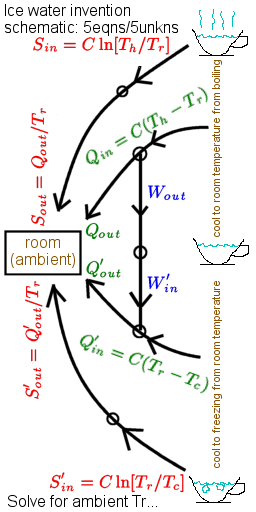
"The change in an object's internal energy equals the disordered-energy (heat) transferred into that object minus the ordered-energy (work) that the object does on its surroundings." In equations, this is oft written as ΔE = ΔQ - Wout where Wout = PΔV.
The ratio of total energy E to kT is the multiplicity-exponent d(S/k)/d(lnE) with respect to energy, as well as the number of base-b units of mutual information lost about the state of the system per b-fold increase in thermal energy. For quadratic systems this is the no-work specific heat Cv/k. More generally, Cv/k is the multiplicity-exponent with respect to absolute temperature, and thus the number of base-b units of mutual information lost about the state of the system per b-fold increase in absolute temperature. Thus for each 2-fold increase in absolute temperature we lose: ~3/2 bits of mutual information per atom in a monatomic gas (given kinetic energies in each of ν=3 spatial directions), ~6/2 bits of mutual information per atom in a metal, more than 18/2 bits of mutual information per water molecule in the liquid (this is huge), and ν/2 bits of mutal information in other systems that obey equipartition. These "no-work" relationships change under conditions of constant pressure, with enthalpy H = E + PV replacing E above. In that case, ideal-gas heat-capacity per molecule becomes Cp/k = 1+ν/2 bits per 2-fold increase in T.
"The mutual information that we share with an isolated system doesn't go up, and hence its entropy doesn't decrease." Neglecting creation or destruction of correlated subsystems, this means that for non-isolated systems into which heat flows that ΔS = ΔQ/T + ΔSirr where the irreversible entropy change ΔSirr ≥ 0 over time.
If one considers "steady-state engines" into and out of which ordered and disordered energy flows while the engine itself stays the same, we can write the first law for engines as Qout + Wout = Qin + Win. The second law then takes the form Qout/Tout - Qin/Tin - ΔIc = ΔSirr ≥ 0 with time. Along with zero increase in subsystem correlations ΔIc, a heat engine has zero Win while a heat pump has zero Wout. These equations put powerful limits on what cannot, and what might, be done. When they don't rule something out, they often leave you with the job of figuring out how to pull it off. For example, they suggest that home heating in winter could be factors of two more efficient if we don't thermalize flame heat directly, and that when cold enough outside the cooking of food might be done at negligible energy cost if we get our act together.
"As an object's reciprocal-temperature approaches ±Infinity, the number of states accessible to it become few so that its entropy approaches zero." Thus as 1/T approaches +∞ (that is T decreases to 0K), and as 1/T approaches -∞ for population inversions in spin systems and lasers (where T>∞), S approaches 0 or at least something small.
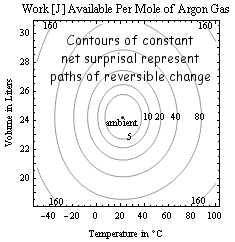
Surprisals add where probabilities multiply. The surprisal for an event of probability p is defined as s=kln[1/p], so that there are N bits of surprisal for landing all "heads" on a toss of N coins. State uncertainties are maximized by finding the largest average-surprisal for a given set of control parameters (say three of the set E, V, N, T, P, μ). This optimization minimizes Gibbs availability in entropy units A=-klnZ where Z is a constrained multiplicity or partition function. When temperature T is fixed, free-energy defined as T times A is also minimized. Thus if T, V and N are constant, the Helmholtz free energy F=E-TS is minimized as a system "equilibrates". If T, P and N are held constant (say during processes in your body), the Gibbs free energy G=E+PV-TS is minimized instead. The change in free energy under these conditions is a measure of available work that might be done in the process. More generally, the work available relative to some ambient state follows from multiplying ambient temperature To by net-surprisal ΔIn≥0, defined as the average value of kln[p/po] where po is the probability of a given state under ambient conditions. From the engine corollary, the work available in thermalizing an object of fixed heat-capacity C from temperature T to ambient To is thus W=ToΔIn. Here net-surprisal ΔIn=CΘ[T/To] where Θ[x]=x-1-lnx≥0. The contours in the figure at right for example, put limits on the conversion of hot to cold as in flame-powered A/C and the ice-water invention depicted above. The economic market value of "specials" is also linked to perceptions about what is "ordinary" (ambient). Mutual information is the average of joint/marginal probabilities kln[pij/pipj] or the net-surprisal that results from learning only that two subsystems are correlated e.g. that DNA molecule strings from two different animals are similar, or that entries in an atlas correspond to stars visible in the night sky. As in the latter example, mutual information can thus help quantify the truth of assertions about the world around.
Mutual information ΔIc on subsystem correlations (in the same units as S) extracts a price in availability, or from the engine corollary ΔIc = Win/To. Thus steady-state excitations, by reversibly thermalizing some ordered-energy to heat at ambient temperature, can support the emergence of a layered series of correlations with respect to subsystem boundaries. Such physical boundaries include gradients (as in the formation of galaxies, stars, and planets), surfaces (as in the context of molecules and multi-cell tissues), membranes (as in the development of biological cells and metazoan skins), and molecular or memetic code-pool boundaries (as in the definition of genetic families and idea-based cultures). Thus, for example, a significant flow of ordered-energy is needed by metazoans who choose to support subsystem-correlations focused inward and outward from the boundaries of self, family, and culture. Molecule and idea codes capable of replication, both discrete and analog, assist with information storage in this process. Thus as non-sustainable free-energy per capita drops, you might expect idea sets to thrive which give short-shrift to some of the boundaries that distinguish observation, belief, consensus, family, friendship, and self.