
This page was assembled to augment the third edition of a book by Louis Bloomfield called How Things Work. However it may also be of more general interest, as part of an emergent-content course designed to do as much as possible with with only everyday math.
Medically useful particles and waves include sound, X-rays, gamma rays and anti-matter electrons from radioisotopes, and radio waves in strong magnetic fields. Quantum phenomena are important to many of these. Here we focus in particular on the subset that depend on a curious process called radioactive decay.
Visualization: Chart of the Nuclides - Notes on Use, Berkeley. Note that nuclei (especially those heavier iron's at Z=26) need more neutrons than protons to be stable as they get larger, to dilute the effects of Coloumb repulsion, even though neither neutrons nor protons can share states because of Pauli exclusion. (Believe it or not, these concepts have already been covered in the course book.)

Radioactive Decay Equation:
fraction_undecayed = 2(-elapsed_time/half_life)
|
f = 2-t/τ = e-t/λ
|

Example Question: Radon 222 (222Ra Z=86), produced when Uranium in rocks decays, emits energetic alpha particles (e.g. 5 MeV Helium nuclei) with a half-life of 3.8 days. The Helium nuclei emitted from Radon would be even more energetic (because of Coulomb repulsion after escaping the strong nuclear force) but for the fact that their escape is made by quantum tunneling i.e. without having to "climb over" the barrier in order to get out. For example, the Illinois Emergency Management Agency Radon program licenses professionals to check the levels of Radon in residential basements. What fraction of the Radon created in rocks under your house makes it into your basement's air, if it takes 1.9 days to diffuse through a barrier coating the bricks in your basement walls? The answer might help you design a more effective diffusion barrier downstream.
Possible Answer: fraction_undecayed = 2(-1.9 days/3.8 days) = 2(-1/2) = 0.707, i.e. 70% is still making it through. If you could design a barrier that takes several half-lives, on the other hand...

Other Examples: Americium 241 (241Am Z=95) emits alphas with a half-life of 432 years. It is used in a subset of ionization smoke detectors. Polonium 210 (210Po Z=84) emits alpha's with a half-life of 138 days. Small amounts of it are commonly used in antistatic brushes. Because the alphas lose energy so fast (even in air) they are not dangerous at a distance, but they can be dangerous up close as the Nov 2006 assassination of Alexander Litvinenko with 210Po in Great Britain suggests.
Tomography is integral to a number of these techniques. This involves recording a shadow image of a person or other object from numerous directions, and then using a mathematical trick to construct from it a 3D model of the object being imaged. This can be done for example using x-rays (CAT scans) or MRI data. Can you determine the 3D structure of this reciprocal lattice model from its rotating shadow?
The relative time and place of two events depends on the location and state-of-motion of the timers, as well as the yardsticks, used to describe it. This results in rather odd behavior for "traveler clocks" moving rapidly with respect to any map-frame of mile-markers and synchronized clocks used to define simultaneity. A familiar map-frame is that defined by earth-based longitude and latitude lines plus a network of clocks on earth's surface synchronized for example to "Central Standard Time".
Time
Dilation Equation:
trav_time/map_time = SquareRoot[1-(trav_speed/lightspeed)2]

|

The time-elapsed on the clocks of a traveler, per unit time-elapsed on clocks in the map-frame, is shown at right for all possible values of traveler speed v (and of kinetic energy K per unit mass m). In map-frame terms, traveler clocks slow as speed goes up. But wait: Does that red line follow a circular path? Precisely. This shows how travelers in effect trade off motion-through-time for motion-through-space as their velocity approaches lightspeed c.
The fastest you've seen a large object moving with respect to you may be the plunge of a comet into the sun at around 0.2% of lightspeed, so that the relative velocities between humans is mostly near the y-intercept. Photons in vacuum, on the other hand, congregate around the x-intercept. As you can see, there is also a lot going on in between. For example, possible nuclear medicine applications were part of the mission of the Bevatron, built in the 1950's in Lawrence Livermore National Labs to give heavy ions more than a billion electron volts of energy per nucleon (rightward of the 1 GeV proton on the plot).
The equation above is a re-arranged version of Minkowski's space-time version of Pythagoras' Theorem...
The Flat-Space Metric Equation:
(light_speed*trav_time)2 =
(light_speed*map_time)2 - (map_distance)2
|
(c Δτ)2 = (c Δt)2 - (Δx)2
|
...which contains virtually all of special relativity's "kinematics" (guidance for describing motion). The metric equation further sets the stage for gravitationally-curved spacetime and accelerated coordinate systems, if one adds a changeable coefficient in front of each term on the right hand side. The effects of this are serious. For example, changing those coefficients (from their flat-space value of one) by only a part per billion is enough to create earth's 9.8 m/s2 acceleration due to gravity. Think how much falling off a chair would hurt if we changed them by only a part per million instead. Ouch!
From the time-dilation graph above you can also see that as velocities approach the speed of light, the proper-velocity ( map-distance traveled per unit traveler-time shown with blue tick-marks on the chart) increases without bound (as does the traveler's momentum to which it is proportional). In fact, the world land-speed record for an accelerated particle on earth is about 100,000 lightyears per traveler-year (ly/ty), as illustrated by this expanded version of the time-dilation plot patterned after anyspeed dynamics plots found two sections hence. Super-colliders do even better by exploiting a multiplicative property of relativistic velocities. They've created collisions between electrons with relative proper velocities near 1010 ly/ty. In this same spirit, one of several calculators for anyspeed constant acceleration problems can be found here.
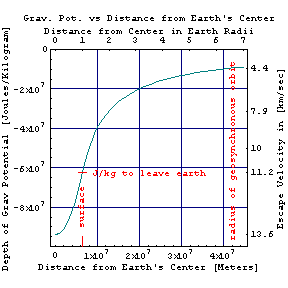
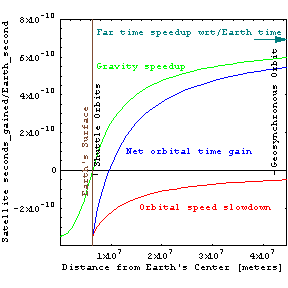
As in the orbital times figure at right, the speedy motion of a satellite in space slows down its clocks relative to ours on earth, while its distance out of the earth's gravitational well (figure above left) makes satellite clocks go a bit faster since grav_time = far_time Sqrt[1-2GM/(c2r)]. Thus shuttle pilots age less than couch potatoes on earth, while geosynchronous orbiters (as well as interstellar dust particles) age more rapidly. This also means that the surface of the earth may be more than a year older than the earth's center, assuming that both were formed at the same time. Although the resulting errors in satellite timing might be measured in nanoseconds, lightspeed is a foot per nanosecond so that the combined effects can result in position errors as large as 15 meters if not taken into account.
Demonstration: Wayne's experiment, using reflections in wires and fiber optics to locate faults, or to estimate light speed.
Although light's wavelength is too large to examine objects much smaller than a biological cell, one method to explore structures on the atomic scale is to toss particles with smaller wavelengths at them, and see which ones collide. The very powerful equation for tracking interactions like these is a spatial version of the equation used above for tracking the variation in time of radioactive decay.
Particle Range Equation:
fraction_uncollided = 2(-traveled_distance/half_range)
|
f = 2-d/R = e-d/λ
|

For this equation, which uses powers of 2, the radioactive decay graph earlier on this page can be easily adapted. That curve can also be relabeled as at left, to use e-folding length or mean free path in the equation, rather than half-range. In that case powers of e ~ 2.71 (the only number whose xth power equals its own slope) are used rather than powers of two. In range-equation form, this curve is used for example to determine how much shielding you need for radiation protection. We also use it in microscopy to determine the thickness of a specimen based on how much of the beam makes it through without being scattered, absorbed, changed in energy, etc.
Particle Wavelength Equation:
momentum=Planck's_constant/particle_wavelength

|
The plot at right shows how the momentum p and kinetic energy K of a particle changes with the wavelength of its wave: Wavelength goes down as momentum and energy go up. The dots correspond to the energy of photons in a radio wave, room temperature heat radiation, visible light, and a dental X-ray. There also a black dot for the 300 kiloVolt electrons that our MIST lab uses to image atoms. As shown here (and in the time dilation plot above), these are just past the midpoint of the elbow which marks the transition to relativistic motion. Note that hydrogen atoms, because they are 1000 times more massive than an electron, have a shorter wavelength at a given kinetic energy. The dark yellow line shows that a 10 nm gold cluster with the same kinetic energy (containing nearly a quarter million gold atoms) has a shorter wavelength still. What does this suggest to you about the wavelength of a charging elephant?
If this plot is extended over a larger range of energies and momenta, it shows that the kinetic energy to accelerate you (not counting your spaceship) to relativistic velocities is about that of an earthquake at 8 on the Richter scale, a gigaton of TNT, or 1011 gallons (more than a thousand supertankers full) of gasoline. In other words, a "jump to lightspeed" by Star Wars' Millenium Falcon probably made it hard to pass up the next chance to refuel. Graph paper on which to plot moving objects of interest to you may be found here and here. Wide uses for kinetic energy versus momentum plots are discussed here. Javascript calculators for these quantities may be found here and here and here.




![[100] bend extinction contour in precipitated VLSI silicon](http://www.umsl.edu/~fraundor/p308tem/Bec100h.jpg)


