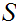 and
and
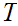 we say that
we say that
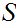 and
and
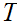 are homotopy equivalent if there exists continuous maps
are homotopy equivalent if there exists continuous maps
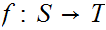 and
and
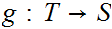 ,
such that ,
,
such that ,
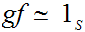
Given topological spaces
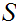 and
and
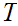 we say that
we say that
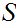 and
and
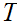 are homotopy equivalent if there exists continuous maps
are homotopy equivalent if there exists continuous maps
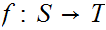 and
and
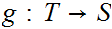 ,
such that ,
,
such that ,
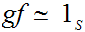
and
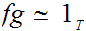
Note:
Homotopy equivalence is an equivalence relation.
Spaces may be homotopy equivalent without being homeomorphic
Example 1
![$\QTR{Large}{[0,1]}$](graphics/homotopyeq__9.png) is homotopy equivalent to
is homotopy equivalent to
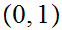 .
Let
.
Let
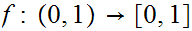 be the inclusion map and
be the inclusion map and
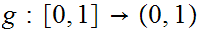 be the constant map
be the constant map
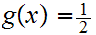
We need to find
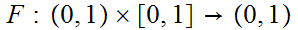 such
that
such
that
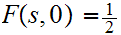 and
and
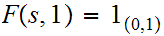 Define
Define
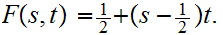 Exactly the same formula works for
Exactly the same formula works for
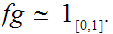
Example
2:
![$\QTR{Large}{[0,1]}$](graphics/homotopyeq__19.png) is not homotopy equivalent to
is not homotopy equivalent to
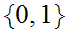
Homework Due April 27 : Prove This.
Suppose there were maps
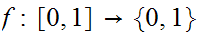 and
and
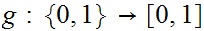
such that
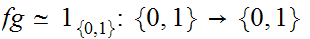 and
and
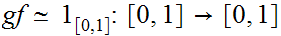
since any map
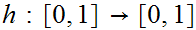 is homotopic to
is homotopic to
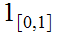 by
the homotopy
by
the homotopy
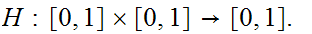 where
where
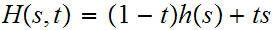
one cannot expect to find a contradiction in this direction. However, since
![$\QTR{Large}{[0,1]}$](graphics/homotopyeq__29.png) is connected we know for all
is connected we know for all
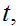
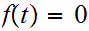 or
or
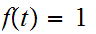 thus
thus
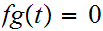 or
or
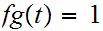
for
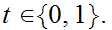 Suppose
Suppose
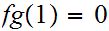 and
and
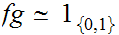 where
where
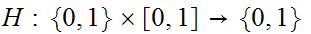 is
the homotopy. Consider
is
the homotopy. Consider
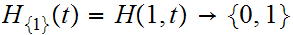
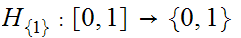 is
a map such that
is
a map such that
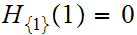 and
and
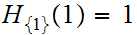 ,
a contradiction.
,
a contradiction.
Example 3: