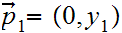 and
and
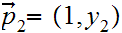 be any two points in the plane such that
be any two points in the plane such that
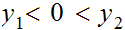 ,
then the segment from
,
then the segment from
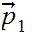 to
to
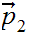 crosses the
crosses the
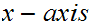 .
.
Let
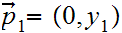 and
and
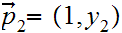 be any two points in the plane such that
be any two points in the plane such that
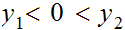 ,
then the segment from
,
then the segment from
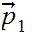 to
to
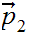 crosses the
crosses the
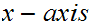 .
.
All points on the segment are of the form
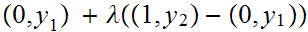 with
with
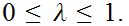
Hence we need to find such a
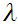 such that
such that
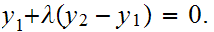 But since
But since
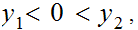
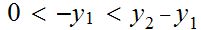
and
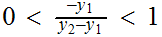
Thus
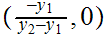 is on the segment from
is on the segment from
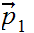 to
to
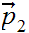 .
.
Let
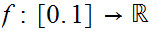 be
any continuous function such that
be
any continuous function such that
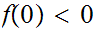 and
and
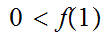 then
there exists some
then
there exists some
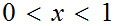 such that
such that
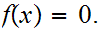
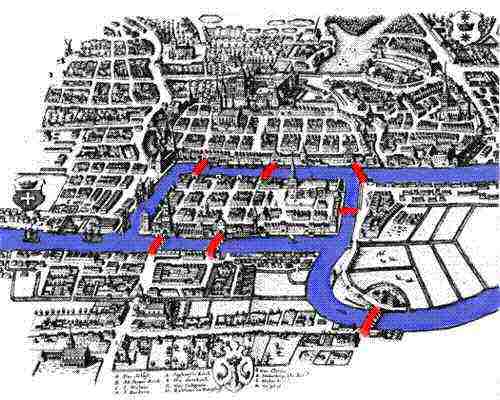
One asks whether or not there a path over the seven bridges that only traverses each bridge once.
It almost goes without saying that the answer to this question has nothing to do with the length of the bridges or the size of the islands. In fact, that no such path exists can be seen from a combinatorial argument rather than an argument about continuity.
To see this, consider the associated Graph:
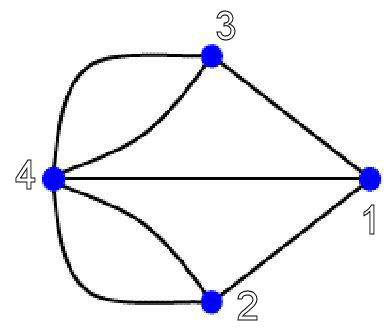
and argue about traversal properties of nodes attached to an even then an odd number of edges.
In a "one-time traverse"
if a node has an even number of edges - a path must both begin and end there, or neither begin nor ends there .
if a node has an odd number of edges - a path must begin there or end there but not both.
Hence, a one-time traverse can have at most two nodes with an odd number of edges (due to Euler).
Since the Seven Bridges of Konigsberg Over the River Pregel problem involves four "nodes" with an odd number of edges, there can not be a one-time traverse.
Another Point of View (Arranging Dominos):
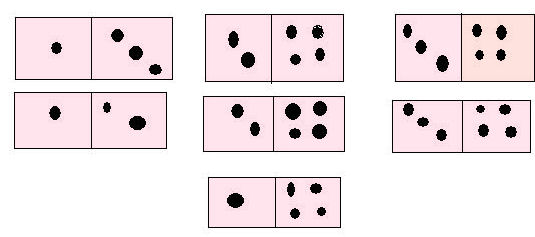
Can we arrange this set of dominos so that they all touch and that touching squares have the same number of dots?
A Connected 1-complex is a connected finite set of line segments, called edges, in the plane that may share common end-points, called vertices, but do not intersect in their interiors.
A 1-complex may or may not divide its complement in the plane into separate regions. Here are some examples:
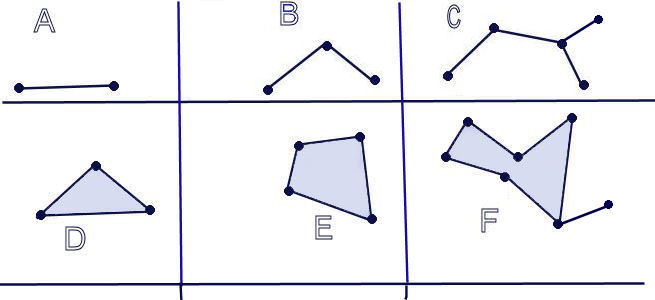
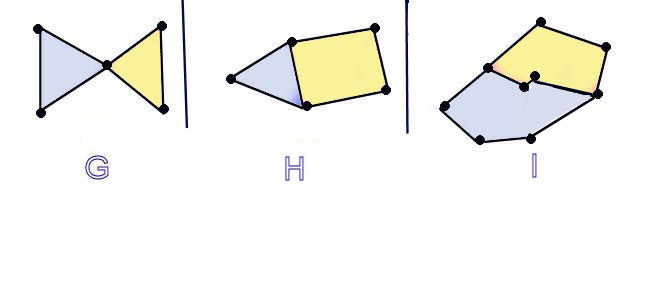
In fact, we can count the number of regions by simply subtracting the number
of vertices from the number of edges and adding
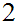 .
.

 #regions
#regions
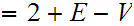
For the examples above:
A.

B.

C..

D.

E.

F.

G..

H.

I.
