One-map two-clock relativity for introductory physics classes

I. Introduction

This is in part due to the facts that: (i) Newton's laws work so well in routine application, and (ii) introductions to special relativity (often patterned after Einstein's introductions to the subject) focus on discovery-philosophy rather than applications. Caution, and inertia associated with old habits, may play a role as well. It is nonetheless unfortunate because teaching Newtonian solutions without relativistic ones at best leaves the student's education out-of-date, and deprives them of experiences which might spark an interest in further physics education. At worst, partial treatments may replace what is missing with misconceptions about the complexity, irrelevance, and/or the limitations of relativity in the study, for example, of simple things like uniform acceleration.

Efforts to link relativistic concepts to classical ones have been with us from the beginning. For example, the observation that relativistic objects behave at high speed as though their inertial mass increases in the p = mv expression, led to the definition (used in many early textbooks {e.g. French}) of relativistic mass m' = m gamma. Such efforts are worthwhile because they can: (A) potentially allow the introduction of relativity concepts at an earlier stage in the education process by building upon already-mastered classical relationships, and (B) find what is fundamentally true in both classical and relativistic approaches. The concepts of transverse (m' ) and longitudinal (m'' = m gamma^3) masses have similarly been used {e.g. Blatt} to preserve relations of the form F_x=ma_x for forces perpendicular and parallel, respectively, to the velocity direction.

Unfortunately for these relativistic masses, no deeper sense has emerged in which the mass of a traveling object either changes, or has directional dependence. Such masses allow familiar relationships to be used in keeping track of non-classical behaviors (item A above), but do not (item B above) provide frame-invariant insights or make other relationships simpler as well. Hence majority acceptance of their use seems further away now {e.g. Adler} than it did several decades ago {Goldstein}.

A more subtle trend in the literature has been toward the definition of a quantity called proper velocity {cf. SearsBrehme, Shurcliff}, which can be written as w = gamma v. We use the symbol w here because it is not in common use elsewhere in relativity texts, and because w resembles gamma v from a distance. This quantity also allows the momentum expression above to be written in classical form as a mass times a velocity, i.e. as p = mw. Hence it serves one of the ``item A'' goals served by m' above. However, it remains an interesting but ``homeless'' quantity in the present literature. In other words, proper-velocity differs fundamentally from the familiar coordinate-velocity, and unlike the latter has not in textbooks been linked to a particular reference frame. After all, it uses distance measured in an inertial frame but time measured on the clocks of a moving and possibly accelerated observer. However, there is also something deeply physical about proper-velocity. Unlike coordinate-velocity, it is a synchrony-free (i.e. local-clock only) {cf. Winnie, Ungar1} means of quantifying motion. Moreover, A. Ungar has recently made the case {Ungar2} that proper velocities, and not coordinate velocities, make up the gyrogroup analog to the velocity group in classical physics. If so, then, is it possible that introductory students might gain deeper physical insight via its use?

The answer is yes. We show here that proper-velocity, when introduced as part of a ``one-map two-clock'' set of time/velocity variables, allows us to introduce relativistic momentum, time-dilation, and frame-invariant relativistic acceleration/force into the classroom without invoking discussion of multiple inertial frames or the abstract mathematics of Lorentz transformation (item A above). Moreover, through use of proper-velocity many relationships (including those like velocity-addition, which require multiple frames or more than one ``map'') are made simpler and sometimes more useful. When one simplification brings with it many others, this suggests that ``item B'' insights may be involved as well. The three sections to follow deal with the basic, acceleration-related, and multi-map applications of this ``two-clock'' approach by first developing the equations, and then discussing classroom applications.

II. A traveler, one map, and two clocks

III. Acceleration and force with one map and two clocks

IV. Problems involving more than one map

V. Conclusions

We show further that a frame-invariant proper acceleration 3-vector has three simple integrals of the motion in terms of these variables. Hence students can speak of the proper acceleration and force 3-vectors for an object in map-independent terms, and solve relativistic constant acceleration problems much as they now do for non-relativistic problems in introductory courses.

We have provided some examples of the use of these equations for high school and college introductory physics classes, as well as summaries of equations for the simple unidirectional motion case (Tables I, II, and III). In the process, one can see that the approach does more than ``superficially preserve classical forms''. Not just one, but many, classical expressions take on relativistic form with only minor change. In addition, interesting physics is accessible to students more quickly with the equations that result. The relativistic addition rule for proper velocities is a special case of the latter in point. Hence we argue that the trend in the pedagogical literature, away from relativistic masses and toward use of proper time and velocity in combination, may be a robust one which provides: (B) deeper insight, as well as (A) more value from lessons first-taught.

VI. Acknowledgments

VII. Appendix A: The 4-vector perspective

VIII. References

IX. Tables

Table I. Equations involving velocities, times, momentum and energy, in classical and two-clock relativistic form.

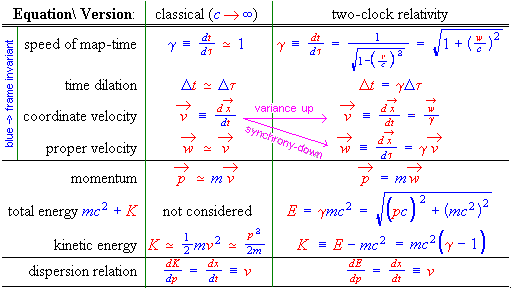
Table II. Unidirectional motion equations involving constant acceleration from rest, and ``2nd law'' dynamics, in classical and two-clock relativistic form. The full (3+1)D version, with equalities valid for any map-frame, differs in that proper force & acceleration are divided by gamma_perp relative to momentum & velocity, but multiplied by gamma_perp relative to energy & dv/dt.

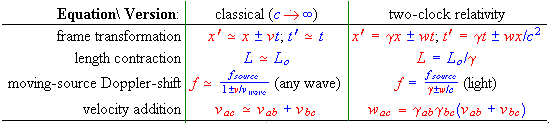
Table III. Unidirectional motion equations involving distances measured in more than one map-frame, in classical and two-clock relativistic form.