I. Introduction
II. A traveler, one map, and two clocks
One may argue that a fundamental break between classical and relativistic kinematics involves the observation that time passes differently for moving observers, than it does for stationary ones. In typical texts, discussion of this fact involves discussion of separate traveler and map (e.g. primed and unprimed) inertial reference frames, perhaps including Lorentz transforms between them, even though the traveler may be accelerated and changing reference frames constantly! This is not needed. Instead, we define two time variables when describing the motion of a single object (or ``traveler'') with respect to a single inertial coordinate frame (or ``map''). These time variables are the ``map'' or coordinate-time t, and the ``traveler'' or proper-time tau. However, only one measurement of distances will be considered, namely that associated with the inertial reference frame or ``map''.It follows from above that two velocities will arise as well, namely the coordinate-velocity v = dx/dt, and proper-velocity w = dx/dtau. The first velocity measures map-distance traveled per unit map time, while the latter measures map-distance traveled per unit traveler time. Each of these velocities can be calculated from the other by knowing the velocity-dependence of the ``traveler's speed of map-time'' gamma = dt/dtau,since it is easy to see from the definitions above that:
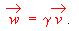 (1)
(1)Because all displacements dx are defined with respect to our map frame, proper-velocity is not simply a coordinate-velocity measured with respect to a different map. However, it does have a well-defined home, in fact with many ``brothers and sisters'' who live there as well. This family is comprised of the velocities reported by the infinite number of moving observers who might choose to describe the motion of our traveler, with their own clock on the map of their common ``home'' frame of reference {Noncoord}. One might call the members of this family ``non-coordinate velocities'', to distinguish them from the coordinate-velocity measured by an inertial observer who stays put in the frame of the map. The cardinal rule for all such velocities is: everyone measures displacements from the vantage point of the home frame (e.g. on a copy of a reference-frame map in their own vehicle's glove compartment). Thus proper velocity w is that particular non-coordinate velocity which reports the rate at which a given traveler's position on the reference map changes, per unit time on the clock of the traveler.
A. Developing the basic equations
A number of useful relationships for the above ``traveler's speed of map-time'' gamma, including it's familiar relationship to coordinate-velocity, follow simply from the nature of the flat spacetime metric. Their derivation is outlined in Appendix A. For students not ready for four-vectors, however, one can simply quote Einstein's prediction that spacetime is tied together so that instead of gamma =1, one has gamma=1/Sqrt{1-(v/c)^2}=E/mc^2, where E is Einstein's ``relativistic energy'' and c is the speed of light. By solving Eqn. 1 for w(v), and putting the inverted solution v(w) into the expression for gamma above, the following string of useful relationships follows immediately:
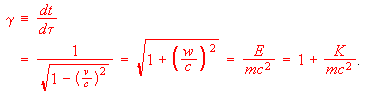 (2)
(2)Because Eqn. 2 allows one to relate velocities to energy, an important part of relativistic dynamics is in hand as well. Another important part of relativistic dynamics, mentioned in the introduction, takes on familiar form since momentum at any speed is
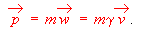 (3)
(3)
B. Basic classroom applications
One of the simplest exercises a student might perform is to show that, as proper velocity w goes to infinity, the coordinate-velocity v never gets larger than speed limit c. This can be done by simply solving Eqn. 1 for v as a function of w. Since student intuition should argue strongly against ``map-distance per unit traveler time'' becoming infinite, an upper limit on coordinate-velocity v may thus from the beginning seem a very reasonable consequence. In typical introductory courses, this upper limit on coordinate-velocity is not something students are given a chance to prove for themselves. Students can also show, for themselves at this point, that classical kinematics follows when all speeds involved obey v << c, since this implies that gamma ~ 1 (cf. Table I).Given these tools to describe the motion of an object with respect to single map frame, another type of relativistic problem within range is that of time dilation. From the very definition of gamma as a ``traveler's speed of map-time'', and the velocity relations which show that gamma >= 1, it is easy for a student to see that the traveler's clock will always run slower than map time. Hence if the traveler holds a fixed speed for a finite time, one has from Eqn. 2 that traveler time is dilated (spread out over a larger interval) relative to coordinate time, by the relation
 (4)
(4)Convenient units for coordinate-velocity are [lightyears per map-year] or [c]. Convenient units for proper-velocity, by comparison, are [lightyears per traveler year] or [ly/tyr]. When proper-velocity reaches 1 [ly/tyr], coordinate-velocity is 1/Sqrt{1+1}=1/Sqrt[2] = 0.707[c]. Thus w=1[ly/tyr] is a natural dividing line between classical and relativistic regimes. In the absence of an abbreviation with mnemonic value for 1 [ly/tyr], students sometimes call it a ``roddenberry'' [rb], perhaps because in english this name evokes connections to ``hotrodding'' (high-speed), berries (minimal units for fruit), and a science fiction series which ignores the lightspeed limit to which coordinate-velocity adheres. It is also worth pointing out to students that, when measuring times in years, and distances in light years, one earth gravity of acceleration is conveniently g = 1.03[ly/yr^2].
We show here that the major difference between classical and two-clock relativity involves the dependence of kinetic energy K on velocity. Instead of (1/2)mv^2, one has mc^2(Sqrt[1+(w/c) ^2] -1) which by Taylor expansion in w/c goes as (1/2)mw^2 when w << c. Although the relativistic expression is more complicated, it is not prohibitive for introductory students, especially since they can first calculate the physically interesting ``speed of map-time'' gamma, and then figure K=mc^2(gamma -1). If they are given rest-energy equivalents for a number of common masses (e.g. for electrons mec^2 ~ 511[keV]), this might make calculation of relativistic energies even less painful than in the classical case!
Concerning momenta, one might imagine from its definition that proper-velocity w is the important speed to a relativistic traveler trying to get somewhere on a map (say for example to Chicago) with minimum traveler time. Eqn. 3 shows that it is also a more interesting speed from the point of view of law enforcement officials wishing to minimize fatalities on futuristic highways where relativistic speeds are an option. Proper velocity tells us what is physically important, since it is proportional to the momentum available in the collision. If we want to ask how long it will take an ambulance to get to the scene of an accident, then of course coordinate velocity may be the key.
Given that proper velocity is the most direct link to physically important quantities like traveler-time and momentum, it is not surprising that a press unfamiliar with this quantity does not attend excitedly, for example, to new settings of the ``land speed record'' for fastest accelerated particle. New progress changes the value of v, the only velocity they are prepared to talk about, in the 7th or 8th decimal place. The story of increasing proper velocity, thus, goes untold to a public whose imagination might be captured thereby. Hence proper-velocities for single 50[GeV] electrons in the LEP2 accelerator at CERN might be approaching w=gamma v=E/mc^2 v ~ 50[GeV]/511[keV] c ~ 10^5[lightyears per traveler year], while the educated lay public (comprised of those who have had no more than an introductory physics course) is under a vague impression that the lightspeed limit rules out major progress along these lines.
III. Acceleration and force with one map and two clocks
IV. Problems involving more than one map
V. Conclusions
VI. Acknowledgments
VII. Appendix A: The 4-vector perspective
VIII. References
IX. Tables
For more on this subject, see our web construction table of contents. Please share your thoughts using our review template, or send comments, answers to problems posed, and/or complaints, to philf@newton.umsl.edu. This page contains original material, so if you choose to echo in your work, in print, or on the web, a citation would be cool.
(Thanks. /philf :)