
...or is there more to the story of vector multiplication than is commonly shared with students in an introductory physics course?
Table of Contents:
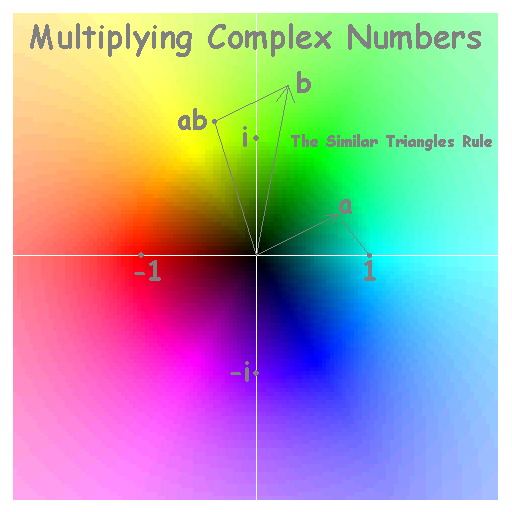
Vectors a and b are added according to the parallelogram rule, labeled in the figure below (following Roger Penrose) as though it is also the rule for adding complex numbers. We've added color to the images to show further how the hue and lightness of a single pixel can be used to uniquely specify a position on the 2D manifold, and then some.

Emboldened by the above image, we might then visualize the mulitvector product of a and b as a directed-arc on a circle of radius ab. This product can be written as ab = a⋅b + a^b = ab Cos[φab] + i ab Sin[φab] = ab ei φab where φab is the angle between a and b. Here a⋅b is the dot or scalar-product of a and b, and a^b is the directed-area bivector for a and b. This latter is like the cross-product a×b (same size and anti-commutivity), except that as a directed-area it "lives in" the plane defined by a and b. The quantity i is the right-angle unit-bivector, whose product with itself is the scalar quantity -1 since "two right angles is a U-turn". The quantity ei φab is a rotor (a unit-circle directed-arc or unit-multivector) which rotates whatever it multiplies by φab.
As you can see from the Penrose visualization below for graphically constructing the complex number (or multivector) product ab, the product of vector a with a unit vector in the "real" direction (a special case of the product relation above) is just the complex number |a|eiφ, where φ is the angle that a makes with that unit vector. In this way bivectors emerge from vector multiplication in 2D as imaginary numbers, which in that disguise have long been helping folks put 2D vectors to use with no mention of vector products per se. Phasor diagrams for the study of AC circuits, and phase-amplitude analysis in the study of spring oscillations and wave optics, are places that you might encounter such quantities in an intro-physics course. Historians may thus say that addition and multiplication of numbers in the "Wessel Argand Gauss complex plane" looks a lot like addition and multiplication of vectors in xy. Perhaps they are one and the same.
Does this mean that 2D vectors and complex numbers are also one and the same? No. Since scalars, vectors, and bivectors are of grade 0, 1, and 2 respectively, vector products in a plane span the even subalgebra (namely scalars and bivectors, or reals and imaginaries) of Euclidean two-space. Vectors in xy span the odd subalgebra. As indicated above, however, multiplication of any vector by a unit reference vector moves it into the even subalgebra, which then acts oddly like a collection of vectors in xy. Below we discuss how such subalgebra mimicry makes tape-measure and time-piece industries quite separate from one another in the (3+1)D world that we live in as well.
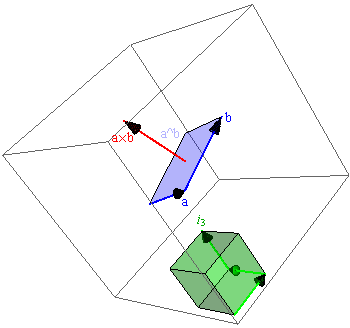
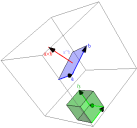
In Euclidean 3-space, one can apply the concepts above on a suitably-oriented planar surface. In that sense the vector product a and b can still be seen as a directed-arc on a planar circle of radius ab. Alternatively, one can use the right-handed orthogonal unit-vectors of a standard Cartesian frame {σx, σy, σz} to define a Cartesian unit-trivector i3 as the directed-volume vector-product σxσyσz. The bivector (or covector) basis in that case can be written as: σxσy = i3 σz, σyσz = i3 σx, and σzσx = i3 σy. Thus the Cartesian unit-trivector i3 lets us define a dual vector-space (a vector set mapped to the bivector or one-form basis) that proves helpful e.g. in the analysis of: gradients, angular momentum, particle scattering, stress/strain, quantized spin, and crystal periodicity. In fact one can show that nature overtly expresses her fondness for such reciprocal or dual spaces in everything from the uncertainty principle (e.g. linking transverse momentum spread in diffraction with our knowledge of "which slit") to the relativistic relationship between time and space (see the next section).
The Cartesian unit-trivector lets us also write the vector product above in 3 dimensions as ab = a⋅b + a^b = a⋅b + i3 a×b. The familiar cross-product a×b (figure at right) is therefore the 3-vector dual to the bivector (or directed-area) a^b. Hence in crystallography, for example, the reciprocal-lattice vector basis {a*,b*,c*} is simply written in terms of direct-lattice basis vectors {a,b,c} via relations like a* = (b×c)/Vc and b* = (c×a)/Vc, where the unit cell volume Vc = a⋅(b×c). Use of cross-products to describe e.g. torques and magnetic forces in intro-physics courses also relies on the idea of vectors that are orthogonal, and in this sense dual, to a directed area. It's helpful to know this, because not all problems involving a directed area can be solved from properties of the cross-product alone. For example bivectors transform differently than vectors, and the wobble of a lopsided football might involve a matrix rather than a scalar moment of inertia.
As with the right-angle unit-bivector i, when multiplied by itself the Cartesian unit-trivector i3 also equals the scalar quantity -1. Hence in vector geometry the square root of minus one has more than one important, and non-imaginary, place to call home.
Vector multiplication in spacetime at the very least makes contact with intro-physics in so far as gravity and magnetism are relativistic effects. To explore this, we start with the oriented unit-hypervolume named in the section title. This dude is the 4D version of "two right turns in a plane". Hence it too yields "-1" when multiplied by itself.

For example, a right-handed set of orthogonal unit-vectors in flat-spacetime {γt, γx, γy, γz} lets one define the Minkowski pseudoscalar I4 as the quadvector product γtγxγyγz. The time-vector γt in this basis-set defines simultaneity for a subset of co-moving objects, which after multiplication by any other spacetime vector (e.g. displacement, or energy-momentum) describes the space-time split in that vector (time vs. space, or mass-energy vs. momentum) as it is experienced by those co-moving objects. In other words, multiplication with an object's time unit-vector γt immediately tosses spacetime vectors into an even subalgebra (or spacetime split) whose scalar, bivector and quadvector elements (reminescent of the 2D case above) masquerade beautifully as a set of spatial 3-vectors parameterized by object scalar time. This is the world that each of us experiences.
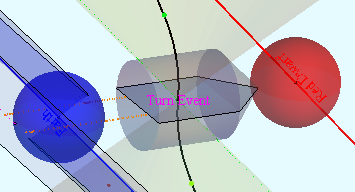
The (2+1)D figure at right plots an accelerated object's time in the vertical direction, and its position in the cyan t=0 plane (xct version here). The little gray spaceship in the center (with orange exhaust) accelerates at 1 gee for 2 years according to onboard clocks, then decelerates for two more so as to pick up some specimens in the red dwarf solar system of Barnard's star 5.52 lightyears away (at the future time of this voyage) before heading back home. The roundtrip takes about 14.5 years on earth clocks. This shows that the relative place and time of events (colored points) in a space-time split changes significantly with the direction of one's time unit vector γt. Earth's view of the same trip is here.
As the animation shows, traveling over 5.5 lightyears in 4 traveler years is facilitated by the spaceship's ability to "length-contract the distance" between Earth and Barnard's star within its space-time split. Intersection between the t=0 plane and the dotted magenta world line marks an interesting location whose distance to the spaceship remains constant during the 1st and 4th quarters of the trip (only in the traveler's split) because the effects of acceleration and contraction cancel out. The energy required for the trip is another story. The top and bottom surfaces of earth's blue lightcone track planes of constant elapsed time on earth. In spite of all the rearrangement going on, the solid black curved world line of the traveler stays within the traveler's yellow future and past light cones. Note also that the proper-time elapsed along the traveler's world line, like the proper-distance between the Earth and red dwarf in their common frame of motion, are "minimally-variant" quantities of more general interest than the space-time split between events and world-lines from other points of view.
Vector products also have many other uses. In the case of displacements, for instance, the time-vector product times its conjugate yields the metric equation or space-time version of Pythagoras' theorem (cdτ)2 = (cdt)2 - (dx)2. This relates the proper time dτ elapsed between two events in the life of a traveler, to the time (dt) and space (dx) intervals measured on a map frame of interconnected yardsticks and synchronized clocks. Part-per-billion shifts in the metric equation in turn give rise to gravity on earth. If we instead multiply γt by space-time's electromagnetic field bivector, we find how this bivector breaks down (for those co-moving objects) into separate electric and magnetic field components. This breakdown can be written using the Minkowski pseudoscalar as E + I4 cB, which in turn helps explain quantitatively how moving charges give rise to magnetic fields as a result of the finite lightspeed constant c that connects time and space.