Navigation bar: [carnival] [river] [superball] [collide] [barnpole] [driving] [carousel] [slingshot] [gravity] [bungee] [hispeed] "Go back" to return.
The illustrations below are generally not accompanied by a narrative. That's because we think they offer direct experience, as well as opportunities to take data for analysis, to students in courses that range from conceptual and introductory physics through modern physics and beyond. Hence you supply the narrative. However, we do suggest some possible questions and mention that:
A useful mnemonic for relative motion in
the Newtonian world is: vAC=vAB+vBC,
where e.g. vAB is the vector velocity of object A with respect
to object B.
Note always that: vAB=-vBA and in sums "a
common middle letter cancels out".What follows are not just moving illustrations that anyone can enjoy. They are data streams. Each panel contains on the order of fifty thousand data points. These include afterimages from previous panels as if the display has a long-duration phosphor. Hence rates of change may also be determined from one panel alone. The information in these panels can be used to explore the physical phenomena being examined in a quantitative way, as described in the note below. Thus they are experimental data from a virtual world. As with experimental data from the real world, they can be used to examine the fit to models being illustrated in a given course, as well as deviations from those models that might give rise to better models downstream.
Note: You can freeze the animations by hitting escape on some browsers, so that measurements can be made from the captured stills e.g. by saving them to disk (e.g. after a [Ctrl-PrtSc] copy to Window's Clipboard) and then loading them into the free scientific image analysis program ImageJ. It's good practice for doing detective work on real world videos as well. To reanimate the figures here after hitting escape, you can reload the page. Some more interactive empirical observation exercises may be found here and here.
Empirical observation exercises (EOE's) for instance play an increasing role in AP Physics courses and assessments. Some exercises adapted in 2015 from these "moving perspectives" may be found here. You and your students may also enjoy our JS/HTML5 electron-microscope simulator here. Earlier interactive EOE's may be found here and here.
The above animation illustrates a Ferris wheel problem that Professor Bernard Feldman used on a kinematics test long ago. It basically shows simultaneous views of a ball tossed up and then caught by a Ferris wheel rider from one inertial and two non-inertial points of view. Although Newton's predictions are easier to track from the inertial point of view, it turns out that they still work locally in accelerated frames and curved spacetime if we consider "geometric accelerations and forces" that act on every ounce of an object's being and can be made to disappear by a suitable vantage point change. (Disclaimer: Please stick with only computer versions of this experiment.)
* The animation should run at ~6 frames per second or a wheel rotation rate of ~4.5 rpm.
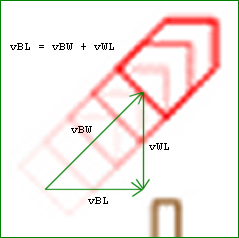The animation above shows the Golden Eagle Ferry
working its way back and forth across the Mississippi
between St. Charles County in Missouri and Calhoun County in Illinois.
As shown at right in the marked up screencap from this animation,
the transverse vector velocity of the boat with respect
to the land (vBL) equals
the 45 degree upstream vector velocity of the boat
with respect to the water (vBW) plus the
downsteam vector velocity
of the water with respect to the land (vWL).
Thus as suggested above, the expression
vBW+vWL equals the quantity
vBL obtained by removing
"W+vW" bracketed by identical
subscripts W from the middle of the former.
In this particular example, the downstream motion of the water
in effect cancels out the upstream component of the boat's motion
in the water.
The following animations illustrate acceleration and/or force vectors from more than one perspective. The illustrations include those coordinate-dependent geometric accelerations and "fictitious" forces that act on every ounce of an object, and that allow Newton's laws to remain locally useful at low speed in accelerated frames as well as in curved spacetime. You'll see further that in high speed situations, without curved spacetime or accelerated frames, that coordinate acceleration and the proper-acceleration felt by a traveler are also not one and the same. Thus the coordinate acceleration of objects in moving and/or accelerated frames includes geometric (frame-dependent) effects that distinguish it from the proper-acceleration caused by the sum of external physical forces.
A draft paper on this topic may be found here.
This illustrates how geometric or "inertial" forces (blue), that are felt in accelerated frames and which act on every ounce of one's being, vanish entirely when one sees the same motion from an unaccelerated perspective. On the other hand the physical forces (red) e.g. of the car on the driver, which act at the point of contact rather than on every ounce of one's being, cannot be made to vanish. At low speeds, these "proper forces" also do not change in magnitude or direction from one frame to the next.
In this example, the "fictitious" geometric force experienced by the carousel rider in the spin frame is correctly described as "centrifugal" or radially-outward. After release of the object, describing the straight line motion in the spin frame is even more complicated even though the map frame perspective sees no forces operating at all!
Map and spin frame perspectives of centripetal (red) and geometric (blue)
forces
on an object released after being spun around on a massless rope,
along
with the reaction force on the rope's anchor point (magenta)
caused by the
centripetal force on the object.
Before the object is released, the blue geometric force is purely centrifugal (pointing radially outward), while after release the geometric force is a sum of centrifugal and Coriolis components. Note that after release in the spin frame that the centrifugal component (light blue) is always radial, while the Coriolis component (green) is always perpendicular to the projectile's velocity in the spin frame.
Note that the rain frame perspective is more like that of a trampoline jumper who tops out just as the ball reaches the edge of the cliff, than it is like the perspective of a raindrop per se. There is of course also a downside to the rain frame perspective, namely that sooner or later the planet you're on gets in the way.
Moving perspectives get even more interesting when high speeds are involved. Times elapsed between events depend on the motion of your clock. Distances between stationary (co-moving) objects may change from some vantage points. Even the sequence of events that are not on the same time-like world line becomes a matter of perspective!
In the animation above, from each perspective a year should elapse about every two seconds or every 100/17.4 frames. However unlike most earlier examples, the panels in the map frame at left are not just translated or rotated versions of those in the traveler frame at right. To begin with, after each round trip ship-pilots on this shuttle-run will have aged only half as much as their starfleet academy classmates stationed on earth. This is time-dilation in action.
To illustrate this, we've chosen to sacrifice panel-by-panel simultaneity. Since traveler and map see the sequence of events differently, there was no unbiased way to keep them in sync anyways. Snapshots associated with individual events can still be compared even if they happen at different times.
Major new differences between panels still abound. These include the distance changes between co-moving stars, seen in the traveler frame. This is length-contraction in action.
Returning to the acceleration theme of this series, note also that the coordinate acceleration (green) seen in the map frame is only significant in the year before and after each launch. The proper-acceleration (red) felt by the traveler is significant throughout the voyage.
We've further added the trace of a light signal initiated from each launch point, but 0.886 map years after launch. This light pulse reaches the traveler at the voyage midpoint to remind them to begin deceleration. Aside: An interesting fact about 1 gee constant proper acceleration is that a year's head start from rest is enough to keep a photon from ever catching you, that is until you either take your foot off the accelerator or you run out of gas. Thus even if the traveler was heading to another galaxy that reminder pulse would have to be sent within the first year.
The light pulse radii are clearly different in the two frames. They illustrate different perspectives on simultaneity. For instance, note in the map frame that Proxima Centauri sees the turnaround pulse before the destination star does, but that the converse is true in the traveler frame. If one could warn the other that it was coming before it got there, of course, we would be able to test who was correct. The large distances involved make this impossible, so that alas the answer to which of two separated events come first, in this case, remains hopelessly dependent on one's point of view. Thankfully both observers do agree about the sequence of events along any time-like world line e.g. during any individual object's history.
Note: In addition to differences between proper and coordinate acceleration at high speeds, proper-velocity (momentum per unit mass w) may be more useful than coordinate speed v. The coordinate speed of such objects is generally near lightspeed, while proper-velocity tells us how rapidly they are covering ground on traveling-object clocks. This is important for example if, like some cosmic ray particles, the traveling objects have a finite lifetime. Proper velocity also clues us in to the object's momentum, which has no upper bound.
For example, a 45 GeV electron accelerated by the Large Electron-Positron Collider (LEP) at Cern in 1989 would have had a Lorentz factor γ of about 88,000 (90 GeV divided by the electron rest mass of 511 keV). Its coordinate speed v would have been about sixty four trillionths shy of lightspeed c at 1 lightsecond per map second. On the other hand, its proper-speed would have been w = γv ~88,000 lightseconds per traveler second. By comparison the coordinate speed of a 250 GeV electron in the proposed International Linear Collider[9] (ILC) will remain near c, while its proper-speed will significantly increase to ~489,000 lightseconds per traveler second.
Proper-velocity is also useful for comparing relative velocities along a line at high speed. In this case wAC = γABγBC(vAB+vBC) where A, B and C refer to different objects or frames of reference. For example wAC refers to the proper-speed of object A with respect to object C. Thus in calculating the relative proper-speed, Lorentz factors multiply when coordinate speeds add. Hence each of two electrons (A and C) in a head-on collision at 45 GeV in the lab frame (B) would see the other coming toward them at vAC~c and wAC = 88,0002(1+1) ~ 1.55×1010 lightseconds per traveler second. Thus colliders can explore collisions with much much higher momentum than can fixed-target accelerators.