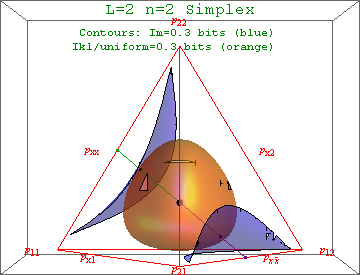
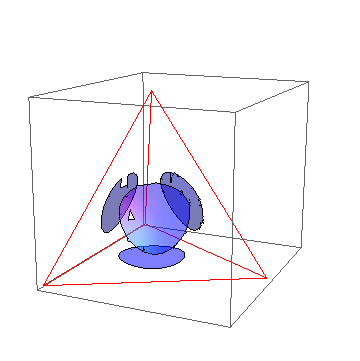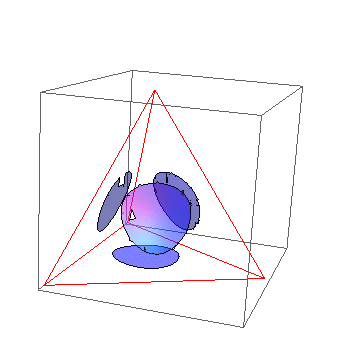
What does the simplex geometry of a layered niche network have to tell us? Let's start simple. Below find a partly labeled view of the L=2 n=2 tetrahedral 3-simplex. This corresponds to a pair of subsystems like coins or half-integral spins, each of which can be in one of only two possible states.
The vertex labels correspond to a single probability set to 1, while the edge labels correspond to a sum of two probabilities set to 1. (The triangular faces correspond to a sum of three probabilities set to 1.) Four of the six edges hold a single probabilty subscript constant, while the other two edges prescribe a relationship between the first and second indices. Can you figure out how to label the vertical edge that faces you, or the horizontal edge on the back side of the model?

The orange "egg" in the center is a contour of constant Kullback-Leibler (KL) divergence with respect to uniform. This is a useful measure of deviation from the center. The blue "saddles" on either side of the egg are contours of constant mutual information, a KL measure of the extent to which the state of subsystem A associated with the first index tells us something about the state of subsystem B associated with the second index.
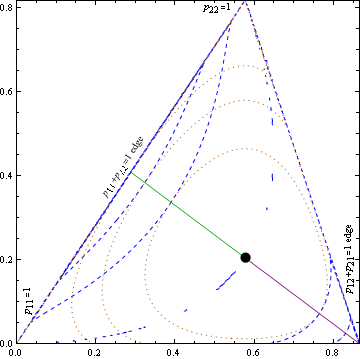
Slicing through the middle of the above tetrahedron, from the vertical edge at left to the bisector of the horizontal edge at right, the figure below shows that orange contours of constant KL divergence with respect to uniform (the pij=1/4 point represented by the black dot) are tangent to surfaces of mutual information along lines (green and purple) of "uniform marginals" which run from 0 bit values at the black dot to 1 bit values at edge bisectors. Intermediate contours here lie at .33 bits and 0.67 bits for both mutual information (blue, dashed) and KL divergence/wrt uniform (orange, dotted).
Interactive models of constant mutual information, and constant KL divergence/wrt uniform, are found here. To what extent can we adapt these lovely geometric pictures of the 3-simplex to the 7-simplex for L=3,n=2 or the 8-simplex for L=2,n=3, or the nL-1 simplex for the general case? For example, we expect in the general case that the system's probability simplex will have nL vertices, and I think nL-1 global mutual-information maxima of (L-1)ln2[n] bits each.
The number of "m-dimensional faces" or facets (themselves regular m-simplexes) on an L-layer n-states/layer simplex is just the binomial coefficient C[nL+1,m+1]=(nL+1)!/((m+1)!(nL-m)!). Here a 0-face is a vertex, a 1-face an edge, a 2-face an equilateral triangle, a 3-face a regular tetrahedron with 4 vertices, a 4-face a pentachoron, a 5-face a hexateron with 6 vertices, a 7-face an octaexon, and a 127 face a regular 127-polytope with 128 vertices, etc. A table of such quantities for selected values of L and n is found below.
|
L |
n |
# pvals (vertices) |
# edges |
# I maxima |
max Im [bits] |
|
2 |
2 |
4 |
6 |
2 |
1 |
|
3 |
2 |
8 |
28 |
4 |
2 |
|
4 |
2 |
16 |
120 |
8 |
3 |
|
5 |
2 |
32 |
496 |
16 |
4 |
|
7 |
2 |
128 |
8128 |
64 |
6 |
Thus the evolution algorithms discussed here are exploring random walks first in a 7 dimensional (L=3 n=2) space, then in a 31 dimensional (L=5 n=2) space, and finally in a 127 dimensional (L=7 n=2) space while maximizing mutual information and monitoring KL divergence/wrt uniform. As one might imagine from the figure above, the walk begins in a direction of increasing KL divergence as well as mutual information, but then finds itself being for some time redirected toward one of the "uniform marginal probability axes" (on a path of decreasing KL divergence) if it did not at random head out in the direction of one to start off.
The evolution process is easy enough to illustrate for the L=2 n=2 case. Here are four paths that evolved toward one of the simplex edges whose bisector corresponds to one bit of mutual information. Can you tell which of the paths involved a significant turnover (see the magenta peak at right) in the level of KL divergence/wrt uniform?
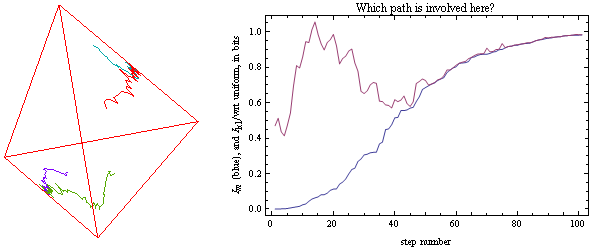
The plot on the left is of course reminescent of the dynamics seen in our first evolution plot. Specifically, the peak in KL divergence with respect to uniform is followed here, as happened there more than once, by a decrease as well as a lowered rate of mutual information increase as the evolution is pulled away from a vertex toward one of the edge maxima. The last third of that evolution plot, which involves random travel in a space of 127 dimensions, of course might be a bit more difficult to visualize. Moreover, there are likely things happening in 127 dimensions that cannot happen in the above 3D model.
For example, our evolution studies indicate that mutual information can get hung up on a local maximum (e.g. in the center of the p122+p212+p221=1 face) when starting from a random position with L>2. (There are no local maxima when L=2, n=2.) Note: When n>2 the global maximum of mutual information may also lie in the center of an m-face with m>1, i.e. on something with more dimensionality than an edge. Understanding this (quantitatively at least) may require a more detailed look at the 7-dimensional L=2, n=3 simplex. The good news (at least for n=2 cases we've examined) is that systems which have reached the mutual information maximum for L layers seem much less likely to get hung up on a local maximum when a new boundary is introduced and the number of random-walk dimensions increases by 2.
On the subject of local maxima in mutual information, it should be easy in
Mathematica to ContourPlot mutual information over a set
of three or four p-values for any L and n settings, mapping the output to
either an equilateral triangle or a regular tetrahedron. What are the
rules for finding local maxima, as well as the rules for determining if they
are global or not?
Consider the L=3,n=2 case. I've now examined values of mutual information on all 56 triangular faces of this 7-simplex. Twenty-four of those faces have two-fold symmetry about edge maxima of 1 bit, eight have three-fold symmetry about a central maximum of 1.36 bits, and another twenty-four are asymmetric and have the global edge maximum of 2 bits as shown below. Caution: Maxima on an m-face are not necessarily real maxima in the probability space of the simplex. For instance, I'm currently working to test the 147 three-fold maximum below. What's the easiest way to determine if a function of 7 variables has a local maximum at a given point?

I also anticipate the possibility of a local maximum in the center of one of the 70 tetrahedral 3-faces. The one case I've checked so far, at p = {{{1/4,0},{0,1/4}},{{0,1/4},{1/4,0}}}, only had a local minimum in mutual information of 1 bit perhaps because it's bounded by four of the eight three-fold symmetric triangles that contain a local maximum. Where would you instead look for a local maximum in the center of a tetrahedron?
Dimension shock: It's still a bit tough to visualize the center of a tetrahedron "exposed to the wind"on the surface of a 7-dimensional object bounded by 70 such tetrahedra, but at least I'm OK with it logically. You'll also note from the figure above that each of the 28 edges (say the 1-4 edge) is shared by six triangles! This is more difficult to do in 3-dimensional space. On the other hand, this observation confirms that the 1-bit edge maxima are not local maxima at all, since on some of the adjacent surfaces in contact with those edges the mutual information continues to increase.
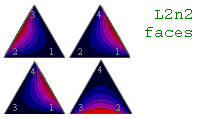
Out of 84 triangular faces, we find 6 black, 6 with a central global maximum, 36 with an edge maximum, and 36 that look like a straight valley is cutting through the center. Examples of these four face types are shown below. In this case, as expected, the global mutual information maximum occurs in the center of a face, because that's when the three states in a given layer are equally probable. Where might we want to look for local maxima?


A routine for calculating the local minimum and maximum of mutual information, as well as location in probability space of the maximum, on all m-faces in this structure should be possible that can compile and compare the resulting lists in reasonable time, at least for modest values of L and n. For example, the L3n3 simplex has 2925 faces, and 10 different face patterns as shown below.
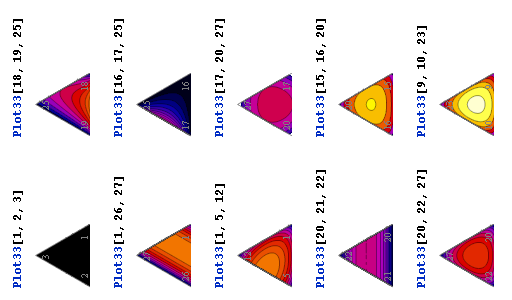
As you can see, three of these may have edge maxima, and four may have face maxima. Given the connection possibilities in spaces of more than 3 dimensions, we've not yet discovered a reliable way to identify which edge/face maxima are local maxima in the full space of possible directions. Likewise for locating maxima which don't lie on 1D or 2D surfaces of the structure. Suggestions are invited for pulling this off...