Hashing Functions and Their
Uses In
Cryptography
Hash Functions and Hashes
Definition: A hash
function is a function that takes a set of inputs of any arbitrary size and
fits them into a table or other data structure that contains fixed-size
elements.
Definition: A hash
is a value in the table or data structure generated by the hash function used
to generate that particular table or data structure. The table or data
structure generated is usually called a hash table. It is also generally
assumed that the time complexity of accessing data in a hash table is O(1), or constant.
Calculating a Hash Table:
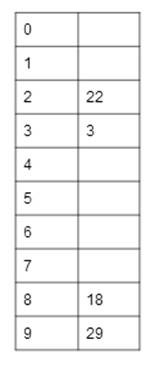
Formal definitions of hash functions vary from
application to application. Letís take a simple
example by taking each number mod 10, and putting it into a hash table that has
10 slots.
Numbers to hash: 22, 3, 18, 29
We take each value, apply the hash function to it, and the result
tells us what slot to put that value in, with the left column denoting the
slot, and the right column denoting what value is in that slot, if any.
Our hash function here is to take each value mod 10. The table to
the right shows the resulting hash table. We hash a series of values as we get
them, so the first value we hash is the first value in the string of values,
and the last value we hash is the last value in the string of values.
22 mod 10 = 2, so it goes in
slot 2.
3 mod 10 = 3, so it goes in
slot 3.
18 mod 10 = 8, so it goes in
slot 8.
29 mod 10 = 9, so it goes in
slot 9.
Collisions
Definition:
A collision occurs when more
than one value to be hashed by a particular hash function hash to the same slot
in the table or data structure (hash table) being generated by the hash
function.
Example Hash Table With Collisions:
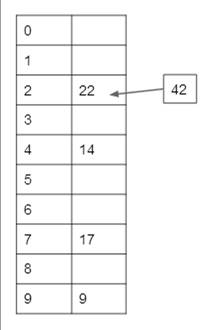 Letís take the exact same hash function from
before: take the value to be hashed mod 10, and place it in that slot in the
hash table.
Letís take the exact same hash function from
before: take the value to be hashed mod 10, and place it in that slot in the
hash table.
Numbers to hash: 22,
9, 14, 17, 42
As before, the hash
table is shown to the right.
As before, we hash
each value as it appears in the string of values to hash, starting with the
first value. The first four values can be entered into the hash table without
any issues. It is the last value, 42, however, that
causes a problem. 42 mod 10 = 2, but there is already a value in slot 2 of the hash table, namely 22. This is
a collision.
The
value 42 must end up in one of the hash tableís slots, but arbitrarly assigning it a slot at random would make
accessing data in a hash table much more time consuming, as we obviously want
to retain the constant time growth of accessing our hash table. There are two
common ways to deal with collisions: chaining, and
open addressing.
Chaining
When
we use chaining to resolve collisions, we simply allow each slot in the hash
table to accept more than one value. Therefore, in the example above, 42 would
simply go in slot 2, as the hash function told us, in a list after 22.
Open Addressing
In open addressing,
collisions in a hash table are resolved by what is known as probing, and the
method of probing can vary, depending on the hash table desired.
One example of
probing is what is known as linear probing. If we apply linear probing to the
example above, the value 42, which our hash function tells us should be placed
in slot 2, will simply be placed in slot 3, since it is empty.
For more information on open addressing, see: http://en.wikipedia.org/wiki/Open_addressing
Effects on Brute Force and The
Birthday Paradox
The Birthday paradox is a classic example of showing
how hashing algorithms reduce the amount of time needed in order to brute-force
an answer. It asks how many people do I need in a room in order to have, to a
certain probability, two people in the same room who have the same birthday
(month and date)? Assuming that all birthdays are equiprobable, we can determine the probability that no two
of n people have the same birthday by the following equation (Wikipedia):
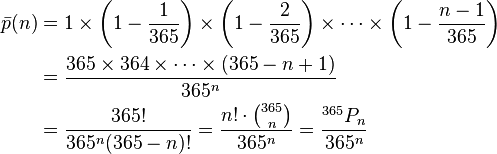
Therefore, the
probability that any two of n people have the same birthday do have the same
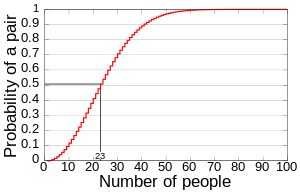
birthday is 1 Ė the answer from the above equation. As the chart below
(Wikipedia) shows, it takes only 23 people to exceed a 50% chance of having two
people in the same room to have the same birthday.
Guaranteeing
Authenticity: Cryptographic Hash Algorithms
Hash
functions can be used to guarantee authenticity of data, if they are designed
to resist attacks from malicious sources. Two such hash functions are RIPEMD-160
and SHA-1.
RIPEMD-160
RIPEMD-160 was
designed to combat against the weaknesses in MD4, MD5, and the 128-bit version
of RIPEMD, and was designed by hans
Dobbertin, Antoon Bosselers, and Bart Preneel.
A reference
implementation of RIPEMD-160 can be found here: http://homes.esat.kuleuven.be/~bosselae/ripemd160.html
C implementation: http://homes.esat.kuleuven.be/~bosselae/ripemd160/ps/AB-9601/rmd160.c
C header file: http://homes.esat.kuleuven.be/~bosselae/ripemd160/ps/AB-9601/rmd160.h
It should be noted that due to SHA-1ís
popularity, RIPEMD-160 has probably not been scrutinized as much as SHA-1 or
other cryptographic hash functions.
SHA-1 (FIPS PUB
180-1)
SHA-1 works on messages
whose length is a multiple of 512 bytes. To account for this, it pads the end
of the message to achieve a message whose length is a multiple of 512. It does
this by first appending a 1 to the end of the message, then a number of 0ís and
then the 64-bit length of the original (unpadded) message. This process will
result in a message whose length is a multiple of 512 bytes.
We also must define
keys to be used during the 80 rounds of the SHA-1 algorithm, which shall be as
follows:
∑
5A827999 for rounds 0 to 19 (0 < t <=
19)
∑
6ED9EBA1 for rounds 20 to 39 (20 < t <=
39)
∑
8F1BBCDC for rounds 40 to 59 (40 < t <=
59)
∑
CA62C1D6 for rounds 60 to 79 (60 < t
<=79)
These are labeled as K≠≠t
in the functions below, where t will denote the current round number.
We also need to define f(B,C,D) for the 80 iterations of SHA-1, which will be
defined as follows. In later parts of the algorithm, this is denoted as ft(B,C,D) where t is the round number.
For rounds 0 to 19, f(B,C,D) = (B & C) | (!B & D)
For rounds 20 to 39, f(B,C,D) = B XOR C XOR D
For rounds 40 to 59, f(B,C,D) = (B & C) | (B & D) | (C & D)
For rounds 60 to 79, f(B,C,D) = B XOR C XOR D
We then process each
512-byte chunk of this message individually, using the following algorithm:
We need two buffers each of five 32-bit
words, and a temporary value. The first buffer will consist of H0, H1,
H≠2, H3, H4, and the second buffer will
consist of A, B, C, D, and E. The temporary value will be named T below.
To begin, we initialize H0 to
67452301, H1 to EFCDAB89, H2 to 98BADCFE, H3
to 10325476, and H4 to C3D2E1F0.
We then let A = H0, B = H1,
C = H2, D = H3 and E = H4.
We then take each 512-byte block of the
message and separate it into 16 32-byte words, W0 to W15.
To compute W17 through W79, use the following equation:
Wt
= (Wt-3 XOR Wt-8 XOR Wt-14 XOR Wt-16)
<< 1, where << denotes a left circular shift.
Then,
to compute the message digest, or SHA-1 hash, we do the following by entering a for loop which goes through 80 iterations (starting at t=0
and ending at t=79):
T
= A << 3 + f(B,C,D) + E + Wt + Kt
(where all addition is addition modulo 232)
E
= D
D
= C
C
= B << 30
B
= A
A
= T
At the very end, the message digest is
simply a concatenation of H0, H1, H2, H3,
and H4.
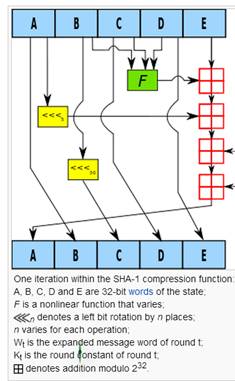
Visualization
of A Round of the SHA-1 Algorithm
Below
is an image which shows what happens to A, B, C, D, and E during one of the 80
iterations of the SHA-1 hash function (Wikipedia):
SHA-3
In
2007, NIST, the National Institute for Standards and Technology, issued a challenge
to the world for anew cryptographic hash function to replace SHA-1 and SHA-2.
In October of 2012, NIST announced Keccak as the
winner of the SHA-3 competition.
The website for Keccak can be found here: http://keccak.noekeon.org/