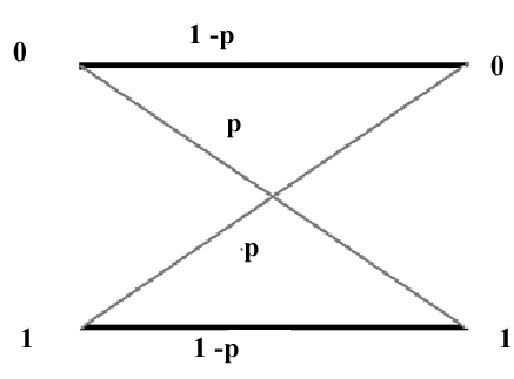

For now we are just considering of a simpler experiment, transmitting a 0 or transmitting a 1 with the possibility of error.
________________________________________________________________________________________________________________
A Bernoulli Trial is an experiment with exactly two possible
outcomes, say
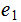 and
and
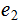 .
If the probability of
.
If the probability of
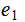 occuring
is
occuring
is
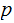 ,
then the probability of
,
then the probability of
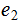 occuring
is
occuring
is
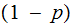 .
.
A Multi-Stage independent Bernoulli Trial
consists of performing the same Bernoulli Trial more than once,
assuming that performing each stage does not affect the outcomes of those that
follows.
Formally, an
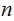 -Stage
independent Bernoulli Trial is a Multi-Stage
independent Bernoulli Trial in which
-Stage
independent Bernoulli Trial is a Multi-Stage
independent Bernoulli Trial in which
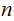 is the number of times the experiment was performed.
is the number of times the experiment was performed.
The Sample Space is the consists of all sequences
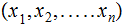 where
where
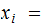
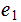 or
or
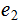 .
.
We will also want to look at the associated Random Variable
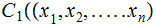
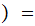 Count
of occurences of
Count
of occurences of
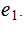
Using the notation above, suppose one performs an n-Stage independent
Bernoulli Trial then the probability that
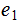 will
occur exactly
will
occur exactly
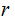 times
is
times
is
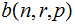 |
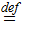 |
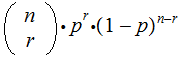 |
referred to as a Binomial Distribution.
Moreover the Expected Value of
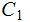 is
is
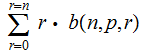
The formula:
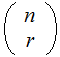 |
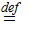 |
|
Properties:
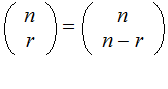
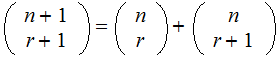
Since
|
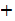 |
 |
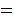 |
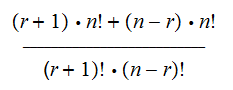 |
 |
|

For any numbers
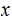 and
and
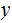 :
:
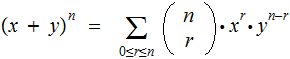
In
particular,
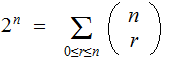
And
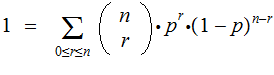
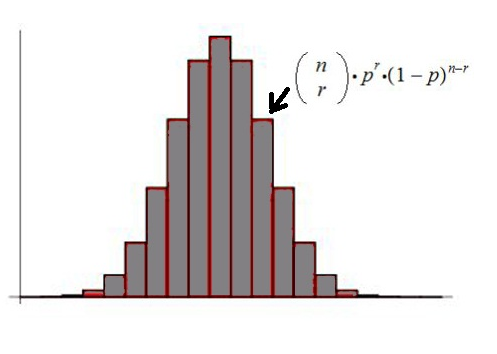
The Calculation:
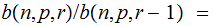
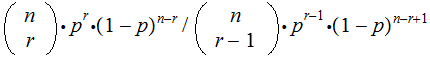
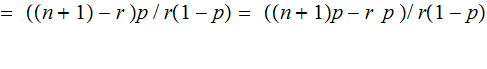
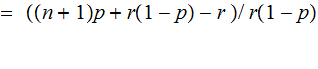
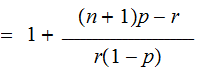
There are two cases to consider:
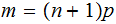 is not an integer:
is not an integer:
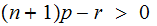 for
for
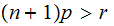 so
so
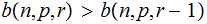
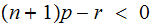 for
for
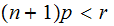 so
so
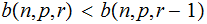
Hence the maximum is an integer near
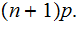
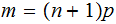 is an integer:
is an integer:
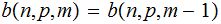 ,
the maximums.
,
the maximums.
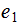 :
:
Theorem :
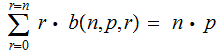
Proof (the hard way):
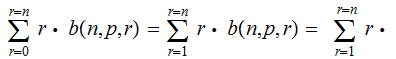
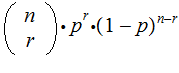
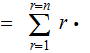
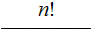 |
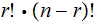 |
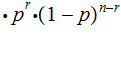
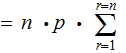
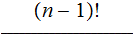 |
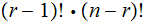 |
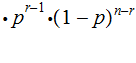
Setting
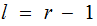
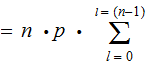
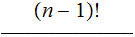 |
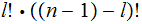 |
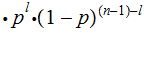
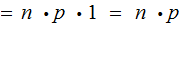
Proof (the easy way):
Exercise: Show if you do the Trial once the expected number
of occurences is
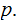 Review
the concept of independent events , in particular that the
expected outcome of independent events is the sum of the expected
Review
the concept of independent events , in particular that the
expected outcome of independent events is the sum of the expected
outcome of the individual events.
Theorem:
Suppose a given a Bernoulli Trial with possible outcomes
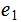 and
and
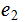 and
and
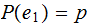 can
be the experiment in an
can
be the experiment in an
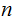 -Stage
independent Bernoulli Trial for any
-Stage
independent Bernoulli Trial for any
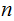 .
Let
.
Let
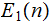 be the number of times
be the number of times
that the outcome is
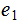 in a given
in a given
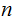 -Stage
independent Bernoulli Trial. Then
-Stage
independent Bernoulli Trial. Then
for any

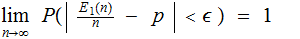 or
or
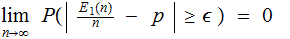
See Bernoulli Trials from the Center for Imaging Science, RIT
Suppose one transmits a Bit and the probability of transmission error is
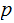
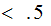 .
As a strategy, a way of improving the chance of correctly transmitting the Bit
is to transmit it 3 times and choose the Bit that comes most
often. Now the probability of error is
.
As a strategy, a way of improving the chance of correctly transmitting the Bit
is to transmit it 3 times and choose the Bit that comes most
often. Now the probability of error is
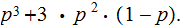 For
example if
For
example if
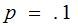 then
the "2 out of 3" probability is
then
the "2 out of 3" probability is
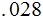 .
If this is not good enough transmit it 5 times. This is not a
very efficient strategy.
.
If this is not good enough transmit it 5 times. This is not a
very efficient strategy.
Exercise: Why does this strategy work?
_________________________________________________________________________________