Intractable problems

From a computational complexity stance, intractable problems are problems for which there exist no efficient algorithms to solve them.

Most intractable problems have an algorithm – the same algorithm – that provides a solution, and that algorithm is the brute-force search.

This algorithm, however, does not provide an efficient solution and is, therefore, not feasible for computation with anything more than the smallest input.

The reason there is no efficient algorithms for these problems is that these problems are all in a category which I like to refer to as “slightly less than random.” They are so close to random, in fact, that they do not as yet allow for any meaningful algorithm other than that of brute-force.

If any problem were truly random, there would not be even the possibility of any such algorithm.

EXAMPLE #1: Factoring a number into primes.

It is the security provided by the lack of any efficient algorithm to solve this problem that allows RSA and public key encryption to be so widely accepted and successful.

EXAMPLE #2: SAT, the satisfiability problem to test whether a given Boolean

formula is satisfiable.

All sets of input must be tried systematically (brute-force) until a satisfying case is discovered.

EXAMPLE #3: Integer partition: Can you partition n integers into two subsets such

that the sums of the subsets are equal?

As the size of the integers (i.e. the size of n) grows linearly, the size of the computations required to check all subsets and their respective sums grows exponentially. This is because, once again, we are forced to use the brute-force method to test the subsets of each division and their sums.

EXAMPLE #4: Graph coloring: How many colors do you need to color a graph

such that no two adjacent vertices are of the same color?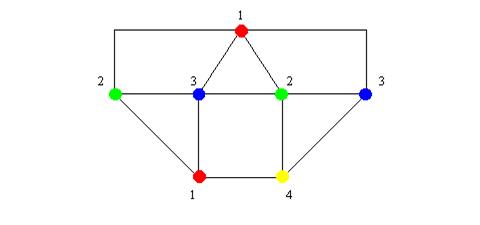

Given any graph with a large number of vertices, we see that we are again faced with resorting to a systematic tracing of all paths, comparison of neighboring colors, backtracking, etc., resulting in exponential time complexity once again.

EXAMPLE #5: Bin packing: How many bins of a given size do you need to hold n

items of variable size?

Again, the best algorithm for this problem involves going through all subsets of n items, seeing how they fit into the bins, and backtracking to test for better fits among subsets until all possibles subsets have been tested to achieve the proper answer. Once again, brute-force. Once again, exponential.