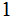 s and
s and
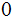 s that a separated by a single blank and with the tape blank elsewhere.
s that a separated by a single blank and with the tape blank elsewhere.
Exercise (Due May 2 ): Build a Turing Machine that
interchanges the position of two strings of
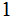 s and
s and
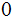 s that a separated by a single blank and with the tape blank elsewhere.
s that a separated by a single blank and with the tape blank elsewhere.
That is, starting with a tape that contains
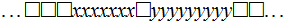 with the Head positioned over the cell containing the initial
with the Head positioned over the cell containing the initial
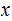 , halts when the tape contains
, halts when the tape contains
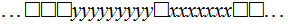 with
the Head positioned over the cell containing the initial
with
the Head positioned over the cell containing the initial
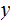 .
.
Hints:
One way to approach this problem is in terms of the Exercise just below, Build the two TMs and combine them.

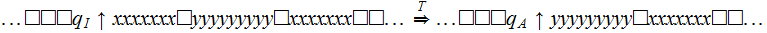
A little care has to be taken because one of the two strings may be empty (or
both, the tape could be blank)
The number of.states or symbols you use for the TM or TMs is not restricted. An symbol marking where the strings start or end might be useful.
For those of you who are building your first TM, It might be useful to build
the machines assuming the
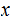 s are
s are
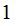 s
and the
s
and the
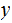 s are
s are
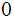 s and then modify the result for the other case.
s and then modify the result for the other case.
Building a TM is like writing any program, starting with an activity diagram or flow chart is usually a good idea.
Answer:
Machine 1.
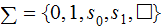 The
present start and end work positions are kept track of using
The
present start and end work positions are kept track of using
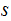 and
and
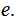
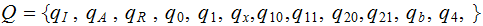
The Transition Function:
The Initial Stage Is the tape blank? Is there only one string?
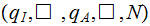 |
The tape is blank, Halt | ||
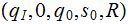 |
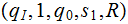 |
Mark the intial symbol | |
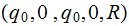 |
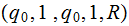 |
Move up the tape | |
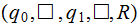 |
Move to the next string?. | ||
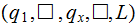 |
There was only 1 string start moving back | ||
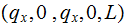 |
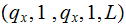 |
||
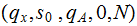 |
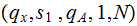 |
Reset the intial symbol |
There are two strings.
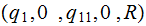 |
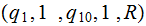 |
The second string is
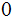 s ,
s ,
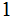 s I need to write
s I need to write
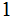 ,
,
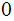 |
|
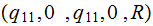 |
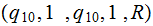 |
Move up the tape | |
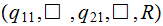 |
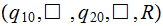 |
Move to the string being written | |
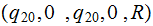 |
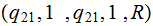 |
Move up the tape | |
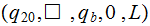 |
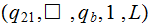 |
Write the symbol and start back down the tape | |
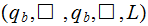 |
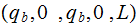 |
Back down the tape to
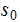 or or
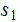 |
|
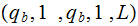 |
|||
(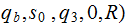 |
(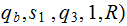 |
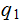 does not quite work.
does not quite work. |
|
(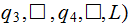 |
Done copying move head to start | ||
(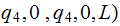 |
(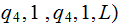 |
||
(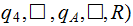 |
|||
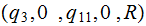 |
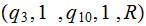 |
Back to the copy mode |
Machine 2. We need to consider the possibility that the tape is empty, the tape contains 1 string, or the tape contains 3 strings.
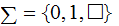 The
present start and end work positions are kept track of using
The
present start and end work positions are kept track of using
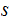 and
and
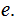
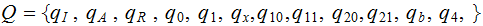
The Transition Function:
The Initial Stage Is the tape blank? Is there only one string?
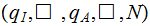 |
The tape is blank, Halt | ||
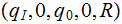 |
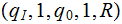 |
Move up the tape. | |
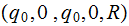 |
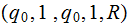 |
Move up the tape | |
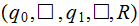 |
Are there more strings? | ||
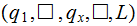 |
There was only 1 string start moving back | ||
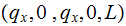 |
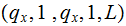 |
||
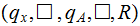 |
Back to the start of the only string. | ||
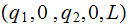 |
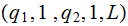 |
Back to the start to remove first string | |
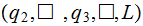 |
Get by the separator blank | ||
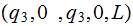 |
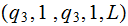 |
||
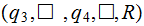 |
Now erase first string | ||
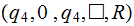 |
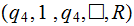 |
||
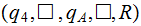 |
Head positioned |
_
Exercise (Due May 2 ): (Informal, again Kolmogorov Complexity )
Given Turing Machines
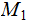 and
and
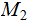 ,
and descriptions
,
and descriptions
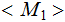 ,
,
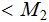 .
.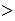 realizing functions
realizing functions
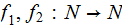 what
would a description for a Turing Machine realizing
what
would a description for a Turing Machine realizing
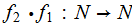 look
like. You answer should, again informally, list a series of general steps
creating the description from any
look
like. You answer should, again informally, list a series of general steps
creating the description from any
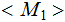 and
and
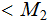 .
.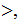 (Hint: How would you do this using Java, or C, or javascript)
(Hint: How would you do this using Java, or C, or javascript)
Answer:
Using the example above create a joined Machine as follows:
Rename all of the states, except
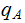 on Machine 2 so that they do not conflict with Machine 1 For example
on Machine 2 so that they do not conflict with Machine 1 For example
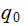 is
renamed
is
renamed
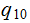 and
and
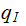 is
renamed
is
renamed
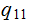
Replace occurences of
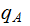 on Machine 1 with the
new
on Machine 1 with the
new 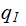 (
(
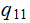 ) from
Machine 2.
) from
Machine 2.
The joined Machine's Transition Function is the union of that of the modified Machine 1 and the modified Machine 2.
In particular, on the joined Machine, if you start "Machine 1" instead of
halting at the old
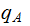 it
starts "Machine 2."
it
starts "Machine 2."
Exercise (Due May 2 ) Verify that the "standard" or simpler short prefix encoding is indeed a prefix encoding.
Answer:
Let
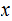
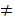
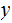 be
two strings
be
two strings
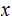 may indeed be a prefix of
may indeed be a prefix of
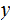 but, using the "standard," they are prefix encoded as
but, using the "standard," they are prefix encoded as
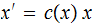 and
and
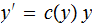
where
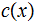 and
and
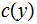 are encodings of the lengths of
are encodings of the lengths of
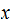 and
and
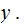 Since
Since 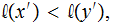 and
and
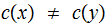 .
,
.
,
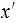 is not a prefix of
is not a prefix of
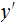 . If
. If
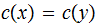 since
since
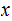
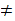
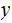 ,
,
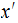
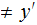
.(Exercise Due May 2) NOT Corollary 6.
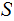
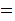
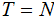 and
and
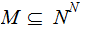 are
the constant functions These are even primitive recursively
enumerable
.
are
the constant functions These are even primitive recursively
enumerable
.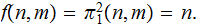
Moreover if
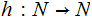 is any function and
is any function and
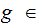
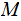 so
is
so
is
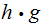 ,
,
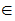
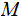 Yet the Theorem itself does not apply. Why?
Yet the Theorem itself does not apply. Why?
Answer:
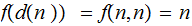 is not a constant function
is not a constant function