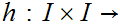
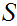 be any function of
be any function of
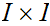 to a topological space
to a topological space
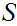 .
Suppose we are given two sequences of reals
.
Suppose we are given two sequences of reals
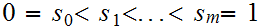
We will need the following:
Lemma
Let
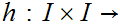
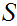 be any function of
be any function of
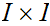 to a topological space
to a topological space
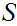 .
Suppose we are given two sequences of reals
.
Suppose we are given two sequences of reals
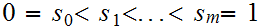
and
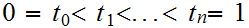 then
then
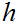 is
continuous if and only if for any
is
continuous if and only if for any
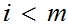 and
and
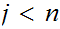 the restriction
the restriction
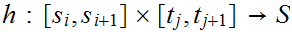 is continuous. We denote this restriction as
is continuous. We denote this restriction as
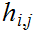
Proof:
That
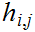 is continuous, given
is continuous, given
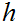 is continuous, is by definition.
is continuous, is by definition.
The other direction is just a special case of the push out lemma. Given the
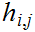 are continuous, note that we are partitioning
are continuous, note that we are partitioning
 as a finite union of closed subspaces so for any closed
as a finite union of closed subspaces so for any closed
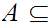
 we have
we have
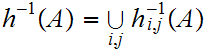 , a finite union of closed sets.
, a finite union of closed sets.
We will work with the covering
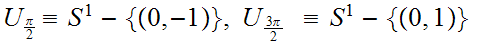 of
of
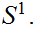 by
two open sets.
by
two open sets.
Since
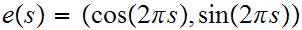 .
.
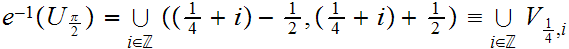
and
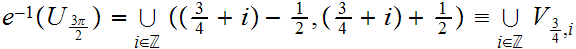
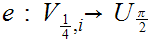 and
and
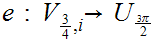 are
homeomorphisms with explicit inverses
are
homeomorphisms with explicit inverses
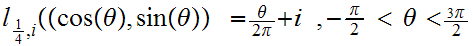
and
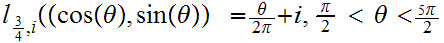
We are identifying
 pairs with suitable "continuous" ranges of angles
pairs with suitable "continuous" ranges of angles
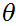
The winding number is invariant under relative homotopy. that is if
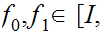
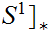 are
relatively homotopic then
are
relatively homotopic then
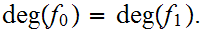
In detail, the hypothesis states that we are given a map
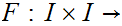
 such
that
such
that
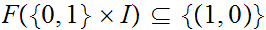 .
That is
.
That is
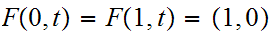 for
all
for
all
Moreover
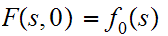 and
and
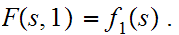
We will show that we can find a map
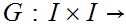
 such
that
such
that
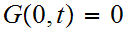 for all
for all
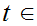
 and
and
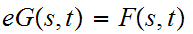 for
all
for
all
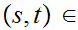

This will prove the theorem since
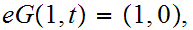 and hence
and hence
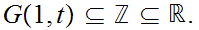
Thus, since
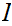 is connected
is connected
 is constant. So
is constant. So
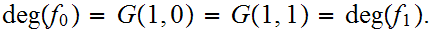
To show that the homotopy
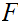 can
be "lifted" to a map
can
be "lifted" to a map
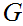 having the given properties.
having the given properties.
Consider the covering
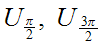 .
.
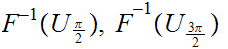 is
a covering of
is
a covering of
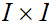 ,
hence has a Lesbegue number
,
hence has a Lesbegue number
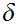 .
Choose any
.
Choose any
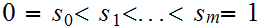 and
and
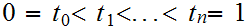 such that
such that
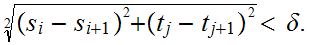 Thus for each
Thus for each
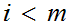 and
and
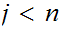
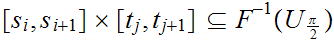 or
or
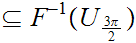 (or both).
(or both).
We now define
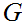 inductively using the sequence
inductively using the sequence
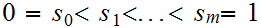
We are given
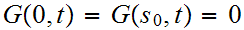 for all
for all
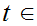
 .
.
Suppose we have defined
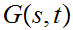 for all
for all

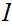
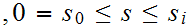 .
.
Fix
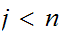 and
for notational simplicity assume that
and
for notational simplicity assume that
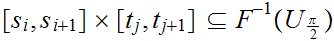 .
.
Since
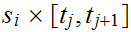 is
connected
is
connected
 . Define
. Define
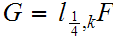 on
on
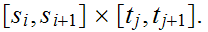
What is left to check is that these maps agree on common edges. But, on common edges, since they start at the same value and cover the same map, this is just requires a restatement of the unique path lifting lemma of last lecture.