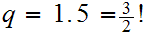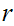 and
and
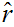 (
(

 and
and

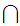
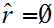 ) such
that:
) such
that:
Since the concept of continuity with respect to the Real Numbers is so central to what follows, a brief review/introduction to the construction of the Real Numbers from the Rationals is in order.
A Dedekind Cut is a partition of the Rational Numbers into
two non-empty sets
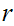 and
and
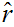 (
(

 and
and

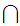
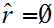 ) such
that:
) such
that:
If
 and
and
 then
then
 .
.
( Hence, if
 and
and
 then
then
 )
)
For every
 there
exists a
there
exists a

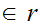 such that
such that

Notes:
Property 2. allows us to avoid the usual ambiguities
caused by the "fact" that
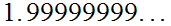 and
and

are the "same" real number.
In general in what follows, rather than explicitly computing
 as the complement of
as the complement of
 , when appropriate we will restrict our definition of a cut to the definition
of
, when appropriate we will restrict our definition of a cut to the definition
of
 .
.
There is a natural inclusion of the Rationals in the Reals.
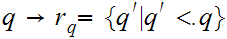
Note, that

The Real Numbers are ordered. (See the example below)
 if the exists a
if the exists a
 such that for all
such that for all
 ,
, 
Or equivalently,
 as sets
as sets
Or equivalently,
 as sets
as sets
One can extend the operation of addition from the Rational Numbers to the Reals.
 and
and
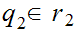

One can extend the operation of negation from the Rational Numbers to the Reals.
For
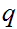 a
Rational, define
a
Rational, define
 .
If
.
If
 for any
for any
 , define
, define


Every set of Real Numbers bounded above has a least upper bound.
One
verifies that, in general,
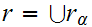 satisfies property 1. and 2.
of the definition of a Dedekind cut.This follows from
satisfies property 1. and 2.
of the definition of a Dedekind cut.This follows from
the fact
that the properties hold for each
 .
.
Now, let
 be a set of Reals and suppose that for all
be a set of Reals and suppose that for all
 .
.
We need
to check that
 is
not empty. But, again, it is a simple argument to show that
is
not empty. But, again, it is a simple argument to show that

A Dedekind Cut is a partition of the Rational Numbers into
two non-empty sets
 and
and
 (
(

 and
and
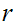

 ) such
that:
) such
that:
To be turned in Tuesday January 34: Complete the proof of 5.
First we need to show that
If
 and
and
 then
then
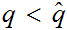 .
.
( Hence, if
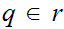 and
and
 then
then
 )
)
For every
 there
exists a
there
exists a

 such that
such that

1. From Boolean Algebra we
know that
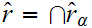
So if

 for all
for all
 .
Hence for all
.
Hence for all
 and all
and all
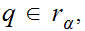 in particular for
in particular for
 , we have.
, we have.
 .
.
2. If
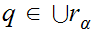 then for some
then for some
 and all
and all
 There there exists a
There there exists a
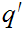
 such that
such that
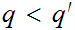
But then

What is left to show is that
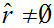 .
But
.
But
 for all
for all
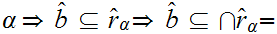
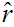 .
.
Finally we show that is a least upper bound.
That it is an upper bound is amounts to observing that
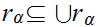

That is a least upper bound follows is also immediate since
 for all
for all
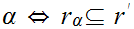 for all
for all
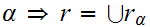
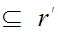

Example:
To show
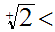
 we need to find some
we need to find some
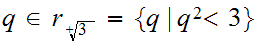 such
that
such
that
 . In particular we need to find
. In particular we need to find
 such
that
such
that
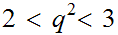 .
.
Let