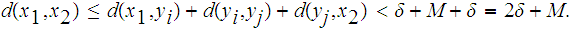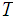 ,
a collection
,
a collection
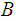 of open subsets of
of open subsets of
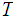 is said to form a basis for the topology on
is said to form a basis for the topology on
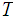 if every open subset of
if every open subset of
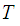 can
be written as a union of sets in
can
be written as a union of sets in
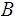 .
.
In a topological space
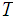 ,
a collection
,
a collection
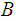 of open subsets of
of open subsets of
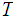 is said to form a basis for the topology on
is said to form a basis for the topology on
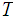 if every open subset of
if every open subset of
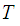 can
be written as a union of sets in
can
be written as a union of sets in
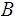 .
.
An open covering of a topological space
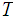 is a collection of open subsets of
is a collection of open subsets of
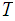 such that every point in
such that every point in
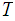 lies in at least one of these open subsets.
lies in at least one of these open subsets.
A topological space
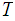 is said to be compact if every open covering of
is said to be compact if every open covering of
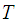 admits
a finite refinement.
admits
a finite refinement.
That is, given any open covering of
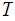 ,
it is possible select a finite subset of the open covering, that still forms
an open covering of
,
it is possible select a finite subset of the open covering, that still forms
an open covering of
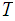 .
.
Any basis is an open covering since
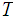 itself is an open set and hence must be the union of basis elements
itself is an open set and hence must be the union of basis elements
An open covering may not be a basis . For example,
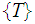 is always an open covering of
is always an open covering of
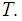
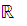 is
not compact.
is
not compact.
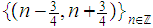 is an open covering without a finite refinement.
is an open covering without a finite refinement.
Every closed subspace
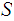 of a compact space
of a compact space
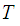 is
also compact.
is
also compact.
Let
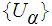 be an open covering of
be an open covering of
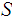 .
Let
.
Let
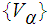 be
a collection of open sets in
be
a collection of open sets in
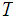 such
that
such
that
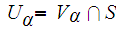 .
.
Since
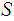 is
closed
is
closed
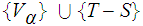 is
a covering of
is
a covering of
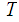 .
.
Since
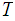 is
compact, let
is
compact, let
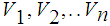 and
possibly
and
possibly
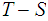 is a finite subcovering of
is a finite subcovering of
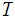 .
Hence
.
Hence
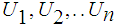 is
a finite subcovering of
is
a finite subcovering of
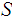 .
.
A subset
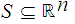 is
bounded if it is contained in some closed
is
bounded if it is contained in some closed
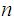 -cube.
That is
-cube.
That is
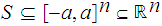
A subset
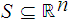 is
compact if and only if is closed and bounded.
is
compact if and only if is closed and bounded.
We will show that
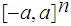 is compact. Thus, since
is compact. Thus, since
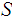 is a closed subset of a compact space it is compact.
is a closed subset of a compact space it is compact.
Now suppose
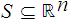 is
compact, we need to show it is closed and bounded.
is
compact, we need to show it is closed and bounded.
To show it is closed, let
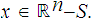 for each point
for each point
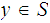 we
can find
we
can find
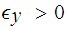 and
and
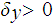 such
such
that
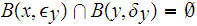 .
.
Since
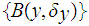 is
an open cover of
is
an open cover of
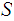 we can find a finite subcover
we can find a finite subcover
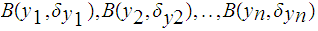 .
.
And since
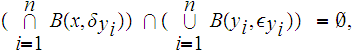 and
and
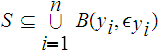 ,
,
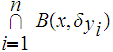 is
a open set containing
is
a open set containing
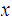 in
in
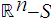 .
Finally, since is
.
Finally, since is
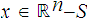 is arbitrary,
is arbitrary,
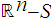 is open so is
is open so is
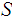 closed.
closed.
To show
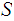 is
bounded, fix
is
bounded, fix
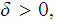 and consider the cover
and consider the cover
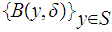 .
Choose a finite subcover
.
Choose a finite subcover
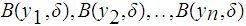 .
Let
.
Let
Homework due March 16:
Show that if
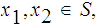
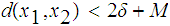 and
hence
and
hence
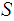 is
bounded.
is
bounded.
Assume
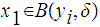 and
and
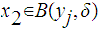 .
.
Then