 "there
exists."
"there
exists."
 "for
every."
"for
every."
 "not"
"not"
 "implies"
"implies"
Logical Notation:
 "there
exists."
"there
exists."
 "for
every."
"for
every."
 "not"
"not"
 "implies"
"implies"
Set Theoretic Notation:
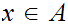 "
"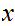 is a member of the set
is a member of the set
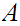 "
"
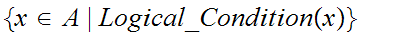 "all
members of
"all
members of
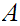 such that
such that
 is true"
is true"
When the
context is clear we write
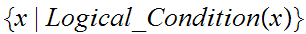
Mathematical Objects of Interest
 The
Natural numbers
The
Natural numbers
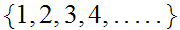
 The
Integers
The
Integers
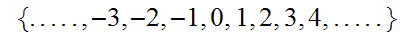
 The
Rational numbers , a set of equivalence classes which can be represented
by
The
Rational numbers , a set of equivalence classes which can be represented
by 
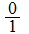 or
or 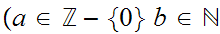 and
and
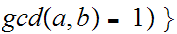

 The
Real numbers (some details to follow)
The
Real numbers (some details to follow)
 The
Algebra of Sets
The
Algebra of Sets
Operations
Given some "universal" set
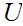 and subsets
and subsets
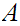 and
and
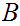 ,
we define:
,
we define:
Union
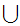
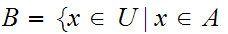 or
or
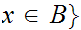
Intersection

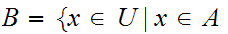 and
and
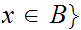
Complement
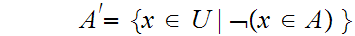
There is also the relationship "Subset"
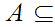
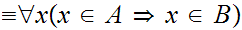
Various Identities:
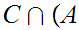
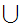
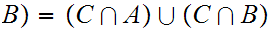
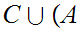
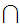
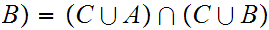
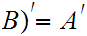
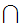
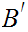
More generally, if
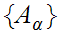 is some indexed set of sets then
is some indexed set of sets then
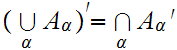
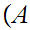
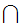
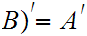
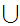
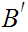
More generally, if
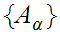 is some indexed set of sets then
is some indexed set of sets then
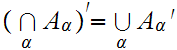
We will want to look at products of sets. That is if
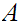 and
and
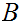 are sets
are sets
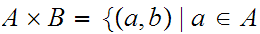 and
and
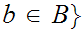
If
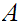 and
and
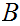 are sets, there is some algebra associated with maps (
functions) from
are sets, there is some algebra associated with maps (
functions) from
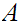 to
to
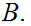
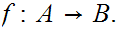
Let
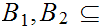
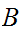 be
two subsets of
be
two subsets of
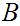 then
then
 1.
1.
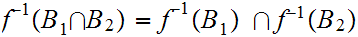
 2.
2.
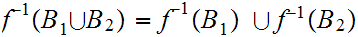
(see the text, Page 12 Lemma 2.8)
Let
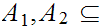
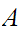 be
two subsets of
be
two subsets of
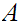 then
then
 3.
3.
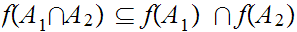
 4.
4.
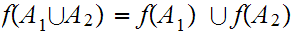
To see that relationship 3.is inclusion rather than
equality consider the situation where
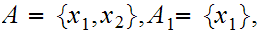
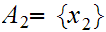
,and 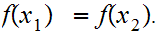 Then
Then
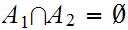 and
and
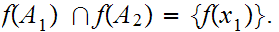
4. is even more immediate.