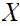 is a binary relation , denoted by the symbol
"
is a binary relation , denoted by the symbol
"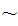 ",
such that for all
",
such that for all
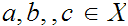
An equivalence relation on a set
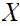 is a binary relation , denoted by the symbol
"
is a binary relation , denoted by the symbol
"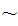 ",
such that for all
",
such that for all
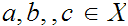
(Reflexivity)
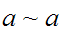
(Symmetry) if
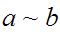 then
then
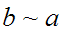
(Transitivity) if
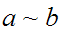 and
and
 then
then
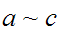
On
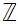 ,
let
,
let
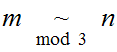 if
if
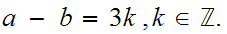
Let
 and
and
 be any to sets. Let
be any to sets. Let
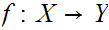 be any function. For
be any function. For
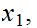
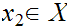 let
let
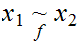 if
if

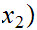
Note that any equivalence relation can be considered as generated by a function onto the set of "equivalences classes."
Let
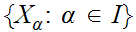 be a family of topological spaces indexed
by
be a family of topological spaces indexed
by .
We consider the unlying sets to be "implicitly" disjoint, in particular we
consider
.
We consider the unlying sets to be "implicitly" disjoint, in particular we
consider
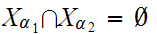 for
for
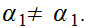 (
Let
(
Let
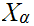 to be the set of pairs
to be the set of pairs
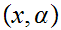 )
)
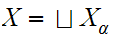
is defined to be the disjoint union of the underlying sets. The topology on
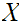 is defined as the finest topology on X for which all injections
is defined as the finest topology on X for which all injections
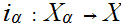
are continuous.
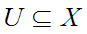 is
open if and only if
is
open if and only if
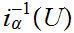 is open for all
is open for all
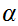 .
.
Given a topological space
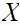 ,
a point set
,
a point set
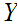 ,
and a function
,
and a function
 which
is onto, we define a topology on
which
is onto, we define a topology on
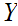 , called the quotient topology under
, called the quotient topology under
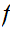 ,
by defining
,
by defining
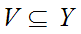 to
be open in the quotient topology if
to
be open in the quotient topology if
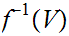 is open in
is open in
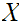 .
.
We can also consider the quotient topology to be the "largest" topology (most
open sets) for which
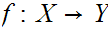 is
continuous.
is
continuous.