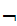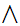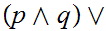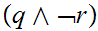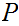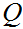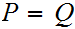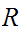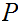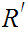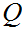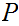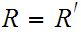The two Boolean constants are
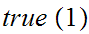 or
or
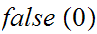 .
.
Boolean variables
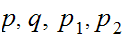 etc,can take on the values
etc,can take on the values
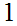 or
or
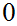 .
.
Boolean constants and Boolean variables are Boolean expressions.
If
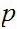 and
and
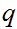 are Boolean expressions, then
are Boolean expressions, then
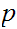
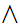
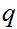 is a Boolean expression, whose truth table is
is a Boolean expression, whose truth table is
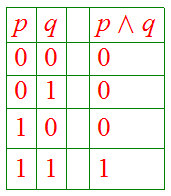 |
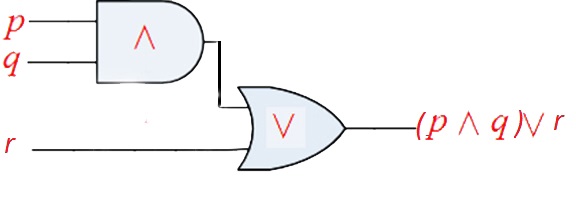
The Gate Diagram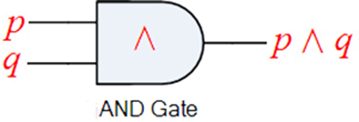 |
If
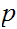 and
and
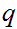 are Boolean expressions, then
are Boolean expressions, then
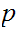
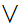
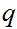 is a Boolean expression, whose truth table is
is a Boolean expression, whose truth table is
 |
The Gate Diagram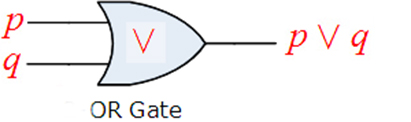 |
If
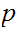 is a Boolean expressions, then
is a Boolean expressions, then
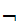
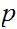 is a Boolean expression, whose truth table is
is a Boolean expression, whose truth table is
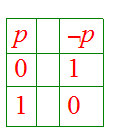 |
The Gate Diagram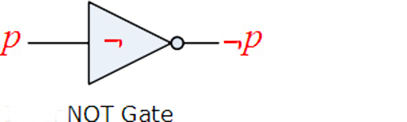 |