Three Applications of Matrix Algebra
Some Code and the Calculation :
int i, j, k, /* misc */
NRA,NRB,NCB; /* number of rows and columns in a and b */
double a[NRA][NCA], /* matrix A to be multiplied */
b[NCA][NCB], /* matrix B to be multiplied */
c[NRA][NCB]; /* result matrix C */
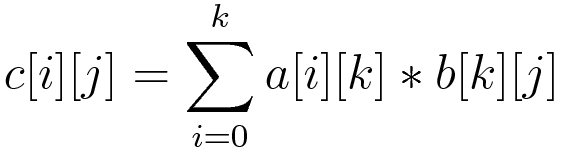
Rotation :
Example:
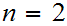
Multiply
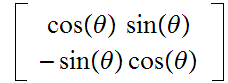 by the vector to be rotated.
.
by the vector to be rotated.
.
A sketch on an application (special effects):
Rotating an image involves rotating the X-Y coordinates of each pixel, 6 rotation computations and some positioning computations( a rotation computation
may not produce an exact x-y pixel position). Roughly, a movie frame has 2 megapixels (2mp), each of which can be though of as
consisting of 3 color bytes and two position bytes. So, setting aside location considerations,
rotating a frame would involve 12 million "position rotation" operations. At 30 frames per second, rotating the images of 1 second of a
movie would involve 360 million operations.
__________________________________________________________________
Markov Processes:
Example: Suppose that the matrix
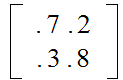 represents
the probabilities that, if it is rainy or sunny on a given day (The Column) it will
be rainy or sunny on the next day (The Row). Suppose that
represents
the probabilities that, if it is rainy or sunny on a given day (The Column) it will
be rainy or sunny on the next day (The Row). Suppose that
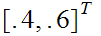 is
the probability that it rainy or sunny on Wednesday, what is the probability
that it will be rainy or sunny on Thursday? Friday?
is
the probability that it rainy or sunny on Wednesday, what is the probability
that it will be rainy or sunny on Thursday? Friday?
Use P(A∧B)=P(A|B)*P(B)
-------------------------------------------------------------------------------------------------------------
Paths and Hops:
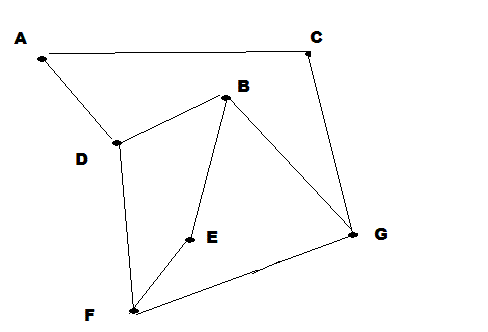
![MATH]()
The associated Matrix of ways to get from one location to another in 1 step:

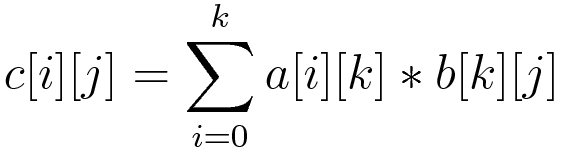
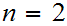
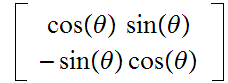 by the vector to be rotated.
.
by the vector to be rotated.
.


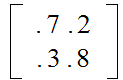 represents
the probabilities that, if it is rainy or sunny on a given day (The Column) it will
be rainy or sunny on the next day (The Row). Suppose that
represents
the probabilities that, if it is rainy or sunny on a given day (The Column) it will
be rainy or sunny on the next day (The Row). Suppose that
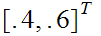 is
the probability that it rainy or sunny on Wednesday, what is the probability
that it will be rainy or sunny on Thursday? Friday?
is
the probability that it rainy or sunny on Wednesday, what is the probability
that it will be rainy or sunny on Thursday? Friday?
