| Where might we expect to find a
conserved quantity X which has been randomly shared between systems for so long that prior information about the whereabouts of X is irrelevant? In other words, where is X likely to be after equilibration? |
The most likely partitioning of X is
that which can happen in the most ways, at which point
all sub-system uncertainty slopes dS/dX become equal
lest the flow of X to higher slope sub-systems persist.
Here accessible states Ω is the number of ways
a (sub-)system might accomodate quantity X, and
uncertainty or entropy S ≡ k ln Ω, where k is
{1, 1/ln2, 1.38×10-23} for S in
{nats, bits, J/K} respectively.
| Ω≡eS/k (#choices=2#bits), and X flows randomly toward larger dS/dX. |
| Solving this for dS/dE gives the equipartition theorem E/N = (ν/2)kT. |
| Solving this for dS/dV gives the ideal gas equation of state PV = NkT. |
| Hence, the product of (ζ/N)b for each reactant goes to one. |
| The 1st law says that the total energy change dE equals heat δQin minus work δWout. |
The 1st law, equipartition, and PV=NkT, can be used to
predict
changes to an ideal gas under various "constraints".
Isobaric changes hold dP to zero (pressure constant).
Isothermal changes hold dT to zero (temperature constant).
Isochoric changes hold dV to zero (volume constant).
Adiabatic changes hold δQ (heat transfer) to zero.
Integral heat capacity E/kT is the exponent of energy
in the expression for multiplicity Ω, while
the differential no-work (e.g. constant volume) heat capacity
CV is the multiplicity exponent of temperature.
At constant pressure, enthalpy H≡E+PV plays the role of E,
while heat capacity at constant pressure is CP=CV+PdV/dT.
Heats of fusion/vaporization associated with bound states
yield first-order phase changes with heat capacities unbound.
| The 2nd law says that entropy δS = δQin/T - δImutual + δSirr where δSirr≥0. |
Isentropic changes hold δS (entropy change) to zero.
Reversible changes hold δSirr to zero.
Also note that extensive variables like E and V add up system contents
while intensive variables like T and P can be measured from point to point.
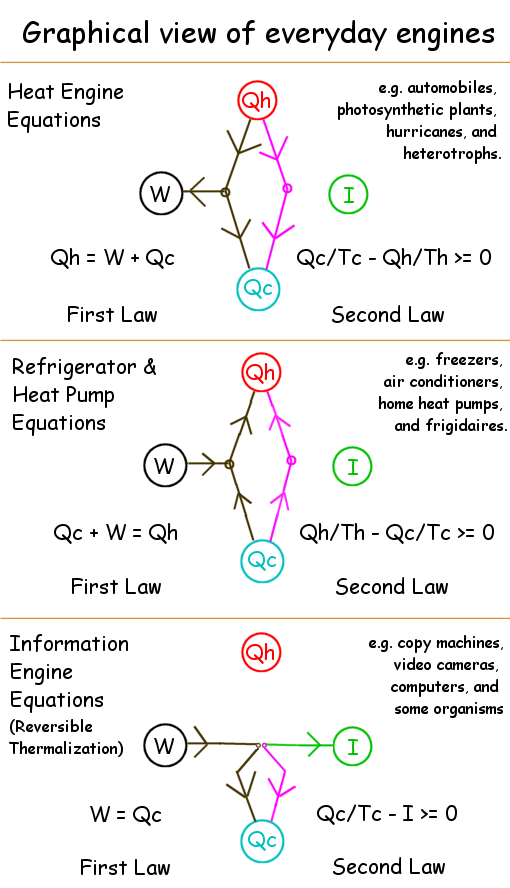
Engines process outside energy via
cyclic alterations of their own state.
Since their own state cycles, the world outside
is where energy-form and correlation changes reside.
| 1st Law: Heat_IN + Work_IN = Heat_OUT + Work_OUT |
| 2nd Law: Uncertainty_INCREASE - Correlation_INCREASE = NetSurprisal_LOST |

A device for cooling hot water is discussed
here,
while the role of reversible thermalization
in the
development of
correlation-based
complexity
(e.g. on our
planet) is illustrated below.

