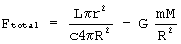
The information available to astronomers has in the past been limited. We now have material in our hands that was formed in carbon-rich Red Giant stars and incorporated into meteorites some 4.5 billion years ago (Bernatowicz et al 1996) . Material identified as presolar isotopically includes nanometer-sized diamonds, micron-sized silicon carbide and graphite particles. We focus here on the spherical graphite particles, referred to as onions because of the concentric (001) graphite layers which form a rim. Most of these particles have a core made up of a novel form of carbon which appears from diffraction as atom-thick (2D) graphite crystals several nanometers in diameter.
It appears that the 3D rim was deposited in the stellar atmosphere after the formation of the 2D core (Fig. 1c) . The rate at which these particles left the star should have been inversely proportional to the time they spent in the region where the 3D graphite was deposited and hence inversely proportional to the thickness of that rim. Experimental dependence of this rim thickness on initial particle size (core diameter) can be tested against radiation pressure models for getting these particles out of the gravitational well of the star in which they were formed.
Data was collected using a Philips EM430 Transmission Electron Microscope (TEM). The sample (KFC1A E) of the Murchison Meteorite was given to me already prepared and ready for use with the TEM. The core and particle slice diameters were determined using two circles on the viewing screen of the TEM, one measuring 5mm and the other 40mm in diameter. I adjusted the magnification until a closest fit to the outer circle was obtained. An estimated value for the core and diameter was then recorded with the corresponding magnification. Eighty three particles were looked at. Pictures were taken at various magnifications to show the orientations of particles to the mount and other particles. Refer to Figs. 1a,1b,and 1c .
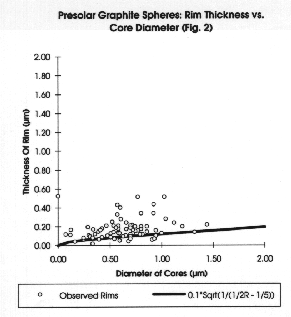
The data can be seen in Fig. 2 . The graph is a plot of slice rim thickness versus slice core diameter. Along with the data a generating function line is also plotted. This is not a best fit line. The data are not expected to follow a line because of variations introduced during the slicing process of sample preparation. If the particles are truly spherical the sample preparation would give us larger cores with small rim thicknesses, and small cores with large rim thicknesses from only a single sphere. It would make sense that we would see more larger particles than smaller ones due to the slicing.
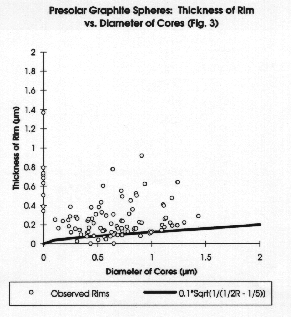
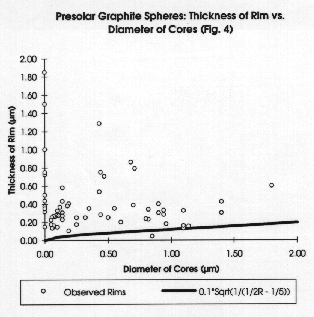
Data from two other sources has also been plotted in the same way, and the graphs are shown in Figs. 3 and 4 . The data in Fig. 3 was collected by Kay Brewer using the same sample I used in my data collection. The data in Fig. 4 was collected by Tom Bernatowicz of a different sample (Bernatowicz et al 1996) . All three figures have the same generating function line drawn on them.
To help us understand the mechanisms that went into creating these particles (onions) let's start with a model in which only the radial forces such as radiation pressure and gravity are considered. We can write the outward force on a particle in free-fall around the star as:
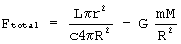
|
L = luminosity of the star G = universal gravitational constant c = speed of light m = mass of the particle (onion) r = radius of the particle M = mass of the star R = distance from the star to the particle |
Assume that the photons are being absorbed rather than reflected by our particle, so that the momentum transferred to our particle per photon is just the energy of the photon E divided by the speed of light c.
Let us determine the maximum radius a particle can have. This can be done by setting the forces of radiation pressure and the gravitational forces equal to zero. We can then determine a maximum radius the particle can have. By writing the mass m of the particle in terms of its radius r and density (Rho), i.e. m=(4/3)r3(Rho), the critical radius can be written like this:
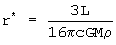
The radial acceleration imposed on the particle by radiation pressure and gravity is a = F total /m from Newton's second law. By substituting for m the above expression in terms of particle radius, we then get an outward acceleration of our particle which can be written as:
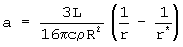
Only shielding of the particle from radiation by intervening dust seems likely to reduce this value. To estimate the time of passage for our particle through an annular shell of thickness (Delta)R surrounding the star, within which carbon can be coated as graphite, we might to first order ignore initial radial and tangential velocities for our particle. In this case, the time elapsed is simply that for traversing a distance (Delta)R from rest under constant acceleration a, or
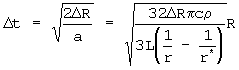
This is an upper limit for a given acceleration, since nonzero inital velocities would be most likely to decrease, not increase, the time of passage. Finally, if D is the effective deposition rate of graphite in the shell of thickness (Delta)R around the star, then the thickness of the graphite layer might be expected to depend on particle size according to the rule:
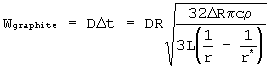
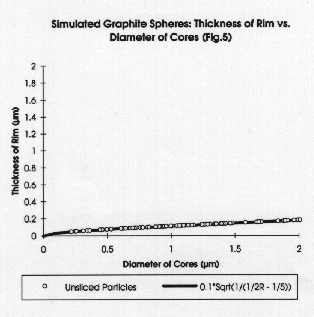
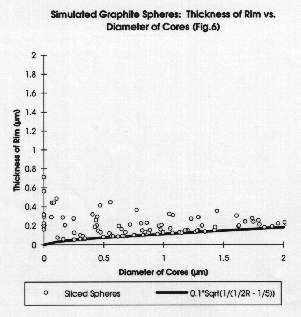
Fig. 5 is a plot of the generating function and a random set of particles before slicing. Fig. 6 is a plot of what might happen to the particles when they are sliced, for comparison with the experimental data.
We have not yet looked at the data collected thoroughly, but we are able, to first order, to estimate some of the parameters. From the graphs we can see that the coefficient in front of the square root is 0.1 (micrometers) 1/2 which means that the equation now looks like this:
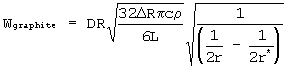
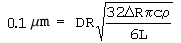
If we plug in a value of one hundredth the radius of the red giant for (Delta)R, the speed of light (3 X 10 8 m/s) for c, one hundred times the luminosity of our sun (4 X10 35 erg/sec) for L, fifty times the radius of the sun (3.5 X 10 7 km) for R, and 2 gm/cm 3 for the density of the particles (Rho), a lower limit on the deposition rate D can be determined, which for the case above, turns out to be about 1 micrometer/1 day (1.16 X 10 -11 m/s). From the deposition rate we can get a value of the minimum pressure required to form these particles, roughly 3 dyne/cm 2 (Bernatowicz et al 1996) . Thus the rim thickness observations, at first glance, support the conclusion by Bernatowicz from the thermodynamics of seed phases found in the cores, namely that gas densities orders of magnitudes above isotropic star values may be needed to form dust particles.
Electron microscope observations of slice core/rim thicknesses for interstellar graphite onions of the Murchison Metorite are reported in a form which facilitates comparison to radiation-pressure ejection models for such particles from the carbon-rich Red Giant atmospheres in which they were likely formed. The data appear consistent with an upward trend in the rim thickness, as a function of core size, although we cannot yet say if there is evidence for the expected square-root dependence. The coefficient which multiplies this root r term suggests that deposition times for the carbon layers in the absence of radiation shielding will be days or less, so that gas densities orders of magnitude above isotropic values may be needed.
Further work will involve a more careful look at slice data, to extrapolate from slice observations back to unsliced particle rim/diameter ratios, and possibly ways to measure core diameters in unsliced particles.
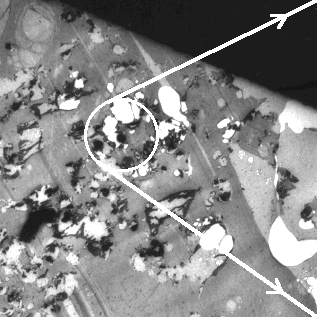
Fig. 1a (300 X Magnification) |
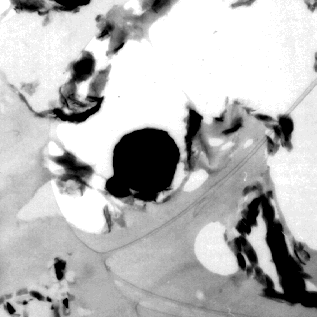
Fig. 1b (4500 X Magnification) |
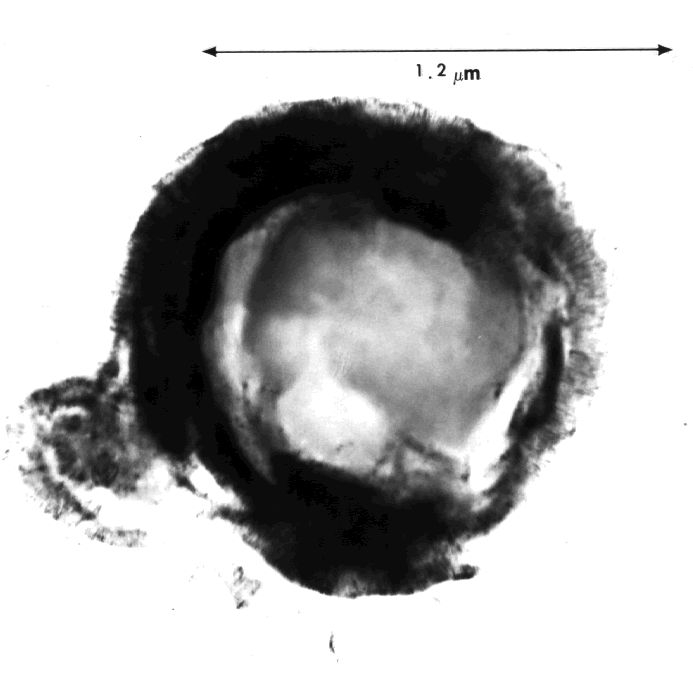
Fig. 1c (35,000 X Magnification) |
|
|
|
|
Bernatowicz T., Ramanath C., Gibbons P., Lodders K., Fegley B., Amari S., Lewis R., "Constraints on Stellar Grain Formation from Presolar Graphite in the Murchison Meteorite", 1996, Astrophysical Journal, 472, 760, 312-G13.