![]()
Now we'll cancel the units (inches with inches, foot with feet)
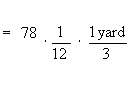
and then multiply the fractions to finish the problem.
![]()
Unit analysis problems involve changing the numbers in a problem from one unit of measurement to another unit of measurement. For example, if I say that my height is 66 inches, I am using inches as my unit of measurement. If I convert 66 inches to feet and then say that I am 5.5 feet tall, I am using a different unit of measurement to express my height.
To convert from one unit of measurement to another, you will have to know some basic facts about the relationships between those units of measurement. Here are some of the facts you should know:
3 feet = 1 yard
5280 feet = 1 mile
60 minutes = 1 hour
24 hours = 1 day
7 days = 1 week
Let's look at some examples of problems in which we must convert from
one unit of measurement to another.
Example 1
Beth wanted to make a tablecloth for her kitchen table. After measuring the table, she decided that the cloth needed to be 78 inches long. How many yards of fabric did Beth need to buy for the tablecloth?
We need to convert from inches to yards. We know that there are 12 inches in one foot; we also know that there are 3 feet in one yard. To do the conversion, we will multiply the original quantity (78 inches) by the appropriate conversion fractions. We will include all of our units of measurement in those fractions, and we will arrange the fractions so that the units of measurement that we no longer want in our final answer will cancel out.
![]()
Now we'll cancel the units (inches with inches, foot with feet)
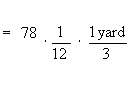
and then multiply the fractions to finish the problem.
![]()
Example 2
If Matthew runs one lap around the track at his school, he has gone a total distance of 400 yards. Yesterday, he ran once around the track in 3 minutes. What was Matthew's running speed in miles per hour?
Right now, Matthew's running speed is expressed in yards per minute. To convert this speed into miles per hour, we will have to convert the distance, 400 yards, into miles, and we will have to convert the time, 3 minutes, into hours.
Let's think about how we'll convert 400 yards into miles. We don't know a direct conversion for yards and miles. But we do know that there are 3 feet in one yard, and we know that there are 5280 feet in one mile, so we'll use both of those conversion fractions in our problem.
To convert 3 minutes into hours, we'll use the fact that there are 60 minutes in one hour.
Arranging the conversion fractions so that the units will cancel gives us the following:
![]()
Now we'll cancel the units (yards with yard, minutes with minutes, feet with feet)
![]()
and then multiply the fractions to finish the problem.
![]()
So Matthew's speed is 100/11 miles per hour (about 4.5 mph).