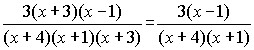First, some general rules to remember:

• Rational expressions (fractions) can only be added or subtracted if they have a common denominator.

• The numerator and denominator of a fraction may be multiplied by the same quantity. This will result in a fraction that is equivalent to the original fraction.

• For a fractional answer to be in final form, the fraction must be reduced to lowest terms.

Adding or subtracting rational expressions is a four-step process:

1. Write all fractions as equivalent fractions with a common denominator.
2. Combine the fractions as a single fraction that has the common denominator.
3. Simplify the expression in the top of the fraction.
4. Reduce the fraction to lowest terms.

Example 1

Step 1: To find a common denominator, start by factoring the denominators of both fractions.

The least common denominator of these two fractions is 2(x+6)(x-6).

Looking at the first fraction, we can see that the factor missing from its denominator is (x-6). In the next step, we'll multiply the top and bottom of the first fraction by (x-6).

Looking at the second fraction, we can see that the factor missing from its denominator is 2. In the next step, we'll multiply the top and bottom of the second fraction by 2.

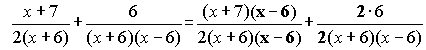
Step 2: Now that the fractions have the same denominators, we'll create one combined fraction by adding the two fractions together:

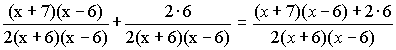
Step 3: We'll simplify the top of the fraction. Notice that we are only simplifying the top of the fraction; the bottom of the fraction remains unchanged.

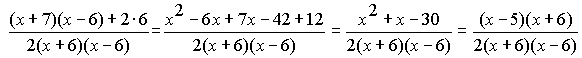
Step 4: Now we'll reduce the fraction to lowest terms

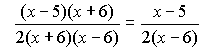
Example 2 
 
 

Step 1: To find a common denominator, start by factoring the denominators of both fractions.

The least common denominator of these two fractions is (x+4)(x+1)(x+3).

Looking at the first fraction, we can see that the factor missing from its denominator is (x+3). In the next step, we'll multiply the top and bottom of the first fraction by (x+3).

Looking at the first fraction, we can see that the factor missing from its denominator is (x+4). In the next step, we'll multiply the top and bottom of the first fraction by (x+4).

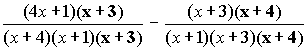
Step 2: Now that the fractions have the same denominators, we'll create one combined fraction by adding the two fractions together:

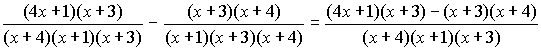
Step 3: We'll simplify the top of the fraction. Notice that we are only simplifying the top of the fraction; the bottom of the fraction remains unchanged.

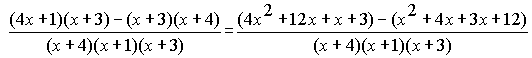
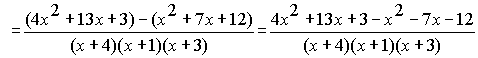
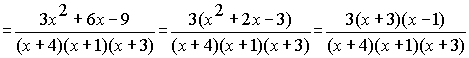
Step 4: Now we'll reduce the fraction to lowest terms