The length of a rectangle is one less than 4 times the width.  If the perimeter is 28 feet, find the dimensions of the rectangle.
 

1. What are we supposed to find in this problem?  The answer to this question is usually found in the last words of the problem.  In this case, we are finding the length and the width of a rectangle.
   
   


2. Let's draw a picture of a rectangle to help define the unknowns (the length and the width).



The problem tells us a lot about the length of the rectangle, but it doesn't say much about the width. Since we don't know much about the width, we'll call the width x. And if the length is one less than 4 times the width, we can then call the length 4x-1. We'll add these variable definitions for the length and the width to our picture:


 
3. Now we'll write an equation for this problem by using the fact that the rectangle's perimeter is 28 feet. First, recall that opposite sides of a rectangle have equal lengths. When we include this information in our picture, we have:



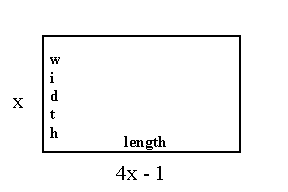
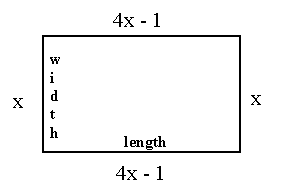
According to the problem, the perimeter of this rectangle is 28 feet. Since perimeter means the distance around an object, we can add the lengths of all four sides of the rectangle to find its perimeter. Adding the sides gives us the equation:

(x) + (4x - 1) + (x) + (4x - 1) = 28


 
4. Now we'll solve our equation:

x + 4x - 1 + x + 4x - 1 = 28

10x - 2 = 28

10x = 30

x = 3

So the width of the rectangle is 3 feet.
 

5. We're not yet finished with this problem. The dimensions of the rectangle include both the width and the length, so we still have to find the length. By looking at our picture, we can see that the length of the rectangle is given by the expression 4x-1, so the length is equal to 4(3)-1=12-1=11 feet.

The dimensions of the rectangle are 3 feet by 11 feet.




Before we leave this problem, let's think about our answer one more time to see if it is consistent with the words of the problem:
 

words	check
The length of a rectangle is one less than 4 times the width.	Our length is 11, and our width is 3. Is 11 equal to one less than the quantity (4 times 3)? Yes!
The perimeter is 28 feet	Our length is 11 and our width is 3. Adding all four sides would give us 11+3+11+3. Does this give us a perimeter of 28? Yes!