Percent of Change Problems
In percent of change problems, some quantity either increases
or decreases from its original number; we must find the percent of change
from the original number to the new number. We'll look at a problem and
solve it using two different methods.
Frank bought a new television set on sale. If the TV's
original price was $200 and Frank paid $170 for the TV, what was the percent
of decrease?
Method 1: A pure algebraic approach
-
The unknown in this problem is the percent of decrease.
A percent of decrease is the percentage of the original price that was
deducted from the original price to obtain the sale price. We could write
a "word equation" for this process like this:
original price - (percent of decrease)(original price)
= sale price
Since the percent of decrease is the unknown in this problem,
we'll call the percent of decrease x%.
Here's what we know so far:
The original price was $200
The sale price was $170
The percent of increase was x%
-
Putting this information in our word equation gives us an
algebraic equation:
200 - (x%)(200) = 170
What do we do with the percent sign in this equation?
"Percent" means "out of 100", so x% means x out of 100, or 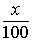 .
Now we have this:
.
Now we have this:
200 - 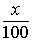 (200)
= 170
(200)
= 170
-
Now we'll solve our equation:
200 - 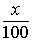 (200)
= 170
(200)
= 170
200 - 2x = 170
-2x = -30
x = 15
So the percent of decrease is 15%
Method 2: A method involving pure arithmetic.
If we know the original price and the sale price, we can
find the percent of decrease in two steps:
-
Find the amount of decrease
-
Divide the amount of decrease by the original amount
This will give us the percent of decrease (written as a decimal
number). We can then write the decimal as an equivalent percent to find
our final answer.
Let's use method 2 on the same problem:
Frank bought a new television set on sale. If the TV's
original price was $200 and Frank paid $170 for the TV, what was the percent
of decrease?
First, let's find the amount of decrease:
Amount of decrease = 200 - 170 = 30
So the price decreased by $30.
Next, we'll find the percent of decrease, and rewrite
the decimal answer as a percent:
Percent of decrease = 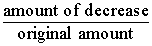 =
= 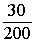 = .15
= 15%
So the percent of decrease is 15%
= .15
= 15%
So the percent of decrease is 15%
Before we leave the problem, let's check our answer:
Original price = $200
Price reduced by 15% of original price = 200(.15) = $30
Sale price would then be = $200 - $30 = $170
Our answer checks. We're done!
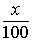 .
Now we have this:
.
Now we have this:
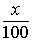 (200)
= 170
(200)
= 170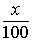 (200)
= 170
(200)
= 170