A Protocol for Deriving Values for DfusHm(298.15 K) and DvapHm(298.15 K).

A Protocol for Deriving Values for D _fusH_m(298.15 K) and D _vapH_m(298.15 K).

Applications in Obtaining D _subH_m (298.15 K)

James Chickos, Gary Nichols, Joe Wilson,

Jennifer Orf, Paul Webb and Jin Wang

Department of Chemistry

University of Missouri-St. Louis

St. Louis MO USA 63121

ABSTRACT. An indirect method for obtaining sublimation enthalpies is described. The method consists of combining experimental or estimated fusion enthalpies adjusted to 298.15 K with either vaporization enthalpies measured at elevated temperatures and adjusted for temperature or obtained directly at 298.15 K by correlation gas chromatography. Some relationships used to adjust phase change enthalpies with temperature are discussed and their use is demonstrated on a series of compounds. These equations are used to adjust the fusion enthalpies of hydrocarbons to 298.15 K. The corresponding fusion entropies at 298.15 K are parameterized using group additivity relationships and the resulting group values are used to estimate fusion entropies and enthalpies at 298.15 K. The techniques discussed are applied to the evaluation of the sublimation enthalpies of perylene and coronene.

1 Introduction

Sublimation enthalpies are an important macroscopic measure of the magnitude of intermolecular interactions in the solid state. Measurement of this quantity serves a variety of useful purposes. This includes uses in thermochemistry as a means of converting condensed phase enthalpies of formation to the gas phase [1], quantifying mass transport by establishing the relationship between vapor pressure and temperature [2], and as an experimental measure of the cumulative effect of the intermolecular forces that lead to the packing observed in the solid state of crystalline materials [3].

A variety of experimental techniques have been developed and applied to directly measure the sublimation enthalpies of solids [4]. Sublimation enthalpies of many other materials cannot be measured directly either because of low volatility or chemical instability. Our recent interests have been focused on the development of methods for obtaining hypothetical phase change enthalpies and entropies that retain their thermodynamic relevance but are measured or derived indirectly. Our attention has focused on experimental as well as estimation techniques.

Sublimation enthalpies have been obtained indirectly by using Eqn. 1. This equation has been used infrequently because vaporization enthalpy data on solids at 298.15 K are not usually available and extrapolations of vaporization enthalpies from measurements performed at elevated temperatures to 298.15 K can be problematic. In addition, Eqn. (1), as written is an approximation. A thermodynamic equality results only

D_subH_m (298.15 K) » D_vapH_m(298.15 K) + D_fusH_m(T_fus) (1)

D_subH_m (298.15 K) = D_vapH_m(298.15 K) + D_fusH_m(298.15 K) (2)

D_subH_m (298.15 K) = D_vapH_m(298.15 K) + (3)

when all three enthalpies are referenced to the same temperature (Eqn. 2), 298.15 K in this case. Eqn. 3 provides a more accurate description in so far as the total phase change enthalpy of the solid, , also includes the enthalpies of all phase transitions occurring between the melting point, T_fus and 298.15 K.

A protocol that adjusts vaporization, sublimation and fusion enthalpies with temperature has been reported recently [5-7]. The use of this protocol is discussed below. Similarly, sublimation enthalpies are generated by combining vaporization enthalpies with experimental fusion enthalpies. The vaporization enthalpies are obtained from the literature or measured indirectly by correlation gas chromatography. Both vaporization and fusion enthalpies adjusted to 298.15 K are used. The results are compared to experimental measurements and evaluated on this basis. In addition, sublimation enthalpy measurements reported on two compounds, perylene and coronene are discussed. The experimental measurements on these two compounds illustrate the difficulties encountered when dealing with high melting samples of low volatility. These physical properties identify an important limitation of the protocol discussed and highlight the useful role that estimation techniques can play. The physical properties of both coronene and perylene have been the subject of recent theoretical treatments [8, 64].

2 Background

2.1. TEMPERATURE ADJUSTMENTS OF D_subH_m AND D_vapH_m

Sublimation enthalpies are very frequently measured at temperatures other than 298.15 K. The temperature of measurement is usually determined by the volatility of the sample of interest. A variety of protocols have been developed to adjust sublimation enthalpies measured at temperature T_m, where T_m represents either a single temperature or the mean of a range of temperatures, back to 298.15 K. The thermodynamic cycle used to adjust sublimation enthalpies from T_m to 298.15 K is illustrated in Figure 1.

D _subH_m(T_m)

Figure 1. Thermodynamic cycle for adjusting sublimation enthalpies to 298.15 K.

If the heat capacities of the gas and solid phase are known, Cp_c and Cp_g, respectively, then the sublimation enthalpy at 298.15 K can be related to experimental measurements by equation 4. This equation, generally referred to as Kirchhoff’s equation, can be used to adjust sublimation enthalpy measurements to any reference temperature. Treating the heat capacities of the two phases as independent of temperature and integrating results in equation 5.

D_subH_m (298.15 K) = D_subH_m(T_m) + (Cp_c - Cp_g)dT (4)

D_subH_m (298.15 K) = D_subH_m(T_m) + (Cp_c - Cp_g) [T_m-298.15] (5)

A diagram similar to Figure 1 (not shown) can also be used to adjust vaporization enthalpies measured at temperature T_m, D_vapH_m(T_m), to 298.15 K. Replacing the sublimation enthalpy terms with the corresponding vaporization enthalpy and substituting the heat capacity of the liquid, Cp_l, for that of the solid, results in Kirchhoff’s equation for liquids, equations 6 and 7.

D_vapH_m (298.15 K) = D_vapH_m(T_m) + (Cp_l - Cp_g)dT (6)

D_vapH_m (298.15 K) = D_vapH_m(T_m) + (Cp_l - Cp_g) [T_m-298.15] (7)

Difficulties associated in using equations 5 and 7 are generally related to the unavailability of an experimental heat capacity, usually for the gas phase and in some instances for the condensed phases as well. Experimental gas phase heat capacities for substances that are solids or liquids at 298.15 K are generally not available. Gas phase heat capacities can be estimated from group additivity methods or calculated from statistical mechanics [9, 10]. Condensed phase heat capacities can be estimated by group methods [11, 12]. In addition, various approximations have been developed. A brief summary of the various methods that have been used in place of equations 5 and 7 are summarized in the Tables 1 and 2.

Table 1. Equations for Temperature Adjustments of Vaporization Enthalpies

Vaporization Enthalpies	Equation	[ref.]
(Cp_l - Cp_g)[T_m-298.15] = 54.4[T_m-298.15]	8	[13]
(Cp_l - Cp_g)[T_m-298.15] = 50.2[T_m-298.15]	9	[14]
(Cp_l - Cp_g)[T_m-298.15] = [10.58 + 0.26Cp_l][T_m-298.15]	10	[15]

Table 2. Equations for Temperature Adjustments of Sublimation Enthalpies

Sublimation Enthalpies, J mol^-1	Equation	[ref.]
(Cp_c - Cp_g) [T_m-298.15] = 2R[T_m-298.15]	11	[4]
(Cp_c - Cp_g)[T_m-298.15] = 6R[T_m-298.15]	12	[16]
(Cp_c - Cp_g)[T_m-298.15] = 40[T_m-298.15]	13	[17]
(Cp_c - Cp_g)[T_m-298.15] = 60[T_m-298.15]	14	[18]
(Cp_c - Cp_g)[T_m-298.15] = [0.75 + 0.15Cp_c(298.15 K)][T_m-298.15]	15	[15]

A major limitation of most of the equations listed in Tables 1 and 2 is that the heat capacity adjustments are treated as universal constants independent of molecular structure. Only equations 10 and 15 are sensitive to differences in molecular structure. These two equations were derived from experimental data that strongly suggested that differences in heat capacities between the condensed and gas phases are dependent both on molecular architecture and size [15]. Heat capacities of the solid or liquid phase are required when using equations 10 and 15; experimental or estimated values can be used.

2.2. A TEST OF TWO HEAT CAPACITY EQUATIONS

Critically evaluated experimental vaporization enthalpies measured at a variety of temperatures generally by calorimetric methods are readily available [19]. The use of equations 7 and 10 in adjusting experimental enthalpies to 298.15 K is illustrated and compared in Table 3. The second column of the table represents the experimental vaporization enthalpy measured at temperature, T_m. The estimated heat capacities of the liquid and gas phase (when available) at 298.15 K are included in the fourth and fifth columns. The heat capacity of the gas and liquid phases were estimated using group additivity methods developed by Benson [10] and Chickos et al. [11], respectively. The adjusted vaporization enthalpies at 298.15 K using equations 7 and 10 are listed in the fifth and sixth columns, respectively. The last column reports the experimental value measured at 298.15 K. Assuming no error in the experimental vaporization enthalpies, the average absolute error between calculated and experimental D_vapH_m (298.15K) using equation 7 and 10 is 1.9% and 1.7 %, respectively. Both equations give equally good results with this limited data set.

Table 3. Adjustment of Vaporization Enthalpies with Temperature

D_vapH_m (T_m)^a

T_m

(K)

Cp_gCp_l

D_vapH_m (298.15K)

estimated

Eqn. 7 Eqn. 10

D_vapH_m (298.15K)^a

C₄H₆ClF₃O 2-chloro-1,1,2-trifluoroethyl ether	32040	368	na^b	212		36627	37500
C₄H₁₀S₂ diethyl disulfide	39250	400	142	208	46024	45806	45170
C₅H₁₀O₂ propyl ethanoate	33940	375	na^b	197		38654	39830
C₆H₅Cl chlorobenzene	34850	405	98.7	155	40866	40250	40970
C₆H₆S benzenethiol	41230	417	106	173	49279	47800	47490
C₆H₁₂O 3-hexanone	35350	397	150	217	41940	41921	42450
C₇H₈O anisole	38880	427	na^b	219		47519	46840
C₈H₁₀ p-xylene	33770	440	128	188	42143	42115	42370
C₁₂H₂₆O 1-dodecanol	84670	343	295	375	88284	89526	91960

^{areference [19]; ^bnot available.

Demonstration of the applicability of equation 15 is more problematic. Temperature adjustments of sublimation enthalpies are smaller than for vaporization enthalpies and the uncertainties associated with many sublimation enthalpies are as large or larger than the adjustment. Consequently, temperature adjustments are barely if ever perceptible above the "noise level" associated with repetitive measurements. This is illustrated in Table 4 for anthracene, a substance whose sublimation enthalpy has be reported numerous times since 1950 and which has been used as a material used to test sublimation enthalpy apparatus [20, 21]. The mean sublimation enthalpy for anthracene from these measurements is 100721 ±
4122 or 100234 ±
4009 J mol^-1depending on whether equation 15 or 5 is used for the temperature adjustment (see Table 5 for Cp values used). The average temperature adjustment is roughly half the uncertainty. As a consequence of this uncertainty, and the fact that heat capacities are not always available, temperature adjustments to sublimation enthalpies have often been ignored. We would like to demonstrate that inclusion of these adjustments, even though small, is important and can lead to significant improvements in accuracy especially when sublimation

Table 4. Sublimation Enthalpies of Anthracene.

D_subH_m(T_m/K)

J mol^-1

T_m/K

(Cp_c-Cp_g)
D
T, J mol^-1

(0.75+0.15Cp_c)
D
T, J mol^-1

D_subH_m(298.15 K), J mol^-1

Eqn. 5 Eqn. 15

[Ref.]

99700

383

1968

2723

101668

102423

[22]

98745

346

1102

1524

99847

100269

[23]

102600 ±
1300

338

924

1279

103524

103879

[20]

94592

376

1805

2499

96398

97091

[24]

91800 ±
3766

303

112

156

91912

91956

[25]

104500 ±
1000

298

0

0

104500

104500

[26]

104766 ±
800

383

1971

2728

106737

107494

[27]

97194 ±
1674

351

1229

1701

98423

98895

[28]

97069 ±
837

298

0

0

97069

97069

[21]

95814 ±
5858

303

112

156

95926

95969

[29]

101035 ±
460

393

2188

3028

103223

104063

[30]

99690 ±
750

393

2200

3044

101890

102734

[30]

98300 ±
560

351

1214

1680

99514

99980

[31]

100834

388

2084

2884

102918

103718

[32]

103400

338

924

1279

104324

104679

[33]

97487 ±
2090

399

2331

3225

99818

100713

[34]

92268 ±
8786

364.15

1121

2118

93799

94386

[35]

101600 ±
2050

347

1531

1552

102721

103152

[33]

enthalpies are evaluated indirectly.
Sublimation enthalpies at 298.15 K can be obtained indirectly by examining the thermochemical cycle illustrated in Figure 2. According to this figure, combining the vaporization enthalpy and fusion enthalpies at 298.15 K also results in D_subH_m(298.15 K). Vaporization enthalpies are available at 298.15 K or can be adjusted to this temperature using equation 10. Since fusion enthalpies are usually measured at either T_fus or at the triple point, it becomes necessary to adjust this enthalpy to 298.15 K. To achieve this result the heat capacities of the solid and liquid phase are necessary. A description of

Figure 2. Thermodynamic cycle for relating phase change enthalpies with temperature.

how fusion enthalpies can be adjusted to 298.15 K by combining equations 10 and 15 follows.
The fusion enthalpy at 298.15 K can be evaluated from the equilibrium value measured at T_fusby correcting for the heat capacity differences between the liquid and solid phases as given by equation 16. It is also necessary to include the enthalpies associated with any additional phase changes occurring between T_fus and 298.15 K (D_pceH_m(T_pc ). As noted above, this is referred to as the solid-liquid phase change enthalpy at 298.15 K (D_slpceH_m(298.15 K)). Treating the heat capacities of the liquid and solid as independent of temperature, results in equation 17. Alternatively, subtracting equation 10 from equation 15 results in an equivalent relationship, equation 18. A comparison of the results obtained in using equations 17 and 18 are provided in Table 4 for a variety of organic compounds.

D_lpceH_m(298.15 K) = D_fusH_m(T_fus) + D_pceH_m(T_pc ) + (Cp_l - Cp_c)dT 16

D_tpceH_m(298.15 K) = D_fusH_m(T_fus) + D_pceH_m(T_pc ) + (Cp_l - Cp_c)(T_fus-298.15) 17

D_tpceH_m(298.15 K) = D_fusH_m(T_fus) + D_pceH_m(T_pc ) +

[(0.75 + 0.15 Cp_c) – (10.58 + 0.26 Cp_l)](T_fus- 298.15) 18
The heat capacities for the solid and liquid phases were estimated as previously described [11]. Heat capacities for the gas phase were estimated using the method described by Benson [10] and as modified by Domalski and Hearing [9]. The lack of necessary group values to estimate the gas phase heat capacities of compounds such as benzoic acid, benzophenone and 2,4-nitrotoluene limits the usefulness of equations 5 and 7. Columns 2 and 3 in Table 5 contain the experimental fusion enthalpy and fusion

Table 5. A Comparison of Equations 17 and 18 in Adjusting Sublimation Enthalpies with Temperature

Compound

D
_fusH

(lit)^a

T_fus

D
_vapH (T_m)

(lit)^b

T_m

Cp_l

Cp_c

Cp_g

D
_subH_m

(298)
Eqn. 7,17

D
_subH_m

(298)
Eqn. 10,18

D
_subH_m

(298)
(lit)

anthracene

29372

489

59390^c

519

279

209

186

95778

97382

100721^d

benzoic acid

18006

396

69189^x

396

212

149

na^w

na^w

89478

89700^e

benzophenone

18194

321

73462^f

353

300

220

na^w

na^w

95263

95570^f

biphenyl

18580

342

61762^g

340

249

192

161

81528

81478

82030^p

2,4-dinitrotoluene

20120^h

343

76862

359

263

227

na^w

na^w

99806

99600^I

2-isopropyl-5-methylphenol

22010^j

324

58442

396

291

220

205

87057

87544

89264^I

naphthalene

19046

353

50246^k

371

205

157

134

71808

71727

72600^l

1,8-octanediol

36100^h

333

101100^m

356

361

262

195

143373

141001

139300ⁿ

phenanthrene

16681^a,o

372

71210^o

372

279

209

186

89576

90241

90880^p

phenol

11514

314

57375

329

177

119

102

70290

70032

69700^q

pyrene

17355^r

424

75640^s

433

295

218

203

95775

97998

100200^t

trans stilbene

27690

397

65460

434

304

235

203

100000

100018

102400^p

1,2,4,5-tetra-chlorobenzene

26340

421

52046

434

228

184

151

83417

82773

83200^u

1,3,5-triphenyl-benzene

22930^v

449

116570^v

477

484

366

327

149861

151756

149499^p

^{areference [36] unless otherwise noted; ^breference [37] unless otherwise noted; ^creference [38]; ^dsee text; ^ereference [40]; ^freference [41]; ^greference [39]; ^hreference [43]; ⁱreference [4]; ^jreference [44]; ^kreference [45]; ^lreference [62]; ^mreference [47]; ⁿreference [48]; ^oreference [49]; ^preference [58]; ^qreference [50]; ^rreference [51]; ^sreference [52]; ^treference [1]; ^ureference [53]; ^vreference [54]; ^wnot available; ^xreference [56].

temperature, while the experimental vaporization enthalpies measured at the mean temperature, T_m, are included as columns 4 and 5. The sublimation enthalpies, adjusted with the aid of equations 7 and 17 and 10 and 18, are included in columns 9 and 10, respectively. A comparison of the standard deviation observed in differences between experimental and estimated values for the entries in Table 5, columns 11 and 9 and 11 and 10, results in standard deviations of ±
2527 and ±
1589 J mol^-1respectively. Both methods give good results. While the number of entries in this table is limited, the use of equation 18 appears to be slightly more accurate in this comparison and more flexible
with regards to its applicability. The use of equations 10, 15 and 18 do not require the heat capacity of the gas phase and this can be an additional advantage if the appropriate group values are not available.

3 Vaporization Enthalpies of Solids at 298.15 K

3.1. APPLICATIONS OF CORRELATION GAS CHROMATOGRAPHY

Correlation gas chromatography has been used to measure the vaporization enthalpies of a large number of organic compounds for which there already exists a reliable database of structurally related materials with known vaporization enthalpies. We have found that the vaporization enthalpies of the n-alkanes serve as suitable standards for hydrocarbons of any structure. The procedure has been detailed previously [55, 6, 7]. A brief outline is provided below using the data in Table 6 as an example. The retention time of carbon tetrachloride as a function of temperature is shown as the first entry. Unlike the other
Table 6. Gas Chromatographic Retention Times

Temperature (K)

543.15

553.15

563.15

573.15

583.15

Compound

Retention
(s)

Time

carbon tetrachloride

46.5

47.58

48.36

48.18

48.48

octadecane

67.62

64.98

62.7

60

58.38

eicosane

82.2

76.32

71.64

66.9

63.9

docosane

105.9

94.38

85.5

77.46

72.12

tetracosane

144.42

123.06

106.98

93.54

84.36

octacosane

306.9

239.52

191.34

154.5

129.42

perylene

348.9

283.02

232.92

192

162.9

coronene

1312.98

984.54

748.74

572.1

448.86

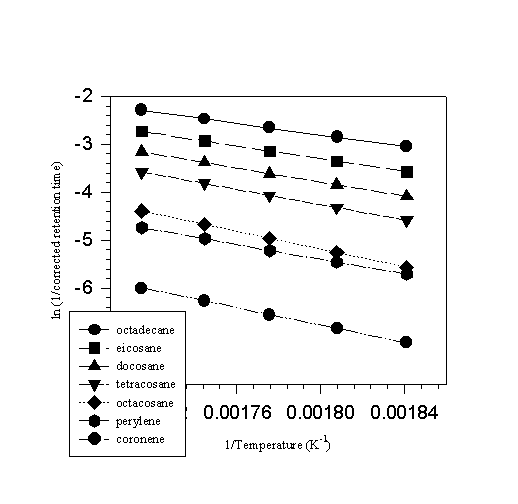compounds, the retention time of carbon tetrachloride is generally observed to increase with increasing temperature. This is characteristic of any material which is not significantly retained on the column and this behavior parallels the increase in viscosity of the carrier gas with temperature which is helium in this case. The retention time of carbon tetrachloride is therefor used to correct for the dead volume of the column. The difference in retention time between each substance and carbon tetrachloride is due to the residence time of the substance on the column. This residence time is inversely proportional to the vapor pressure of the substance "dissolved" in the stationary phase of the column. Furthermore, since the "equilibrium or steady state" established, is between the vapor and "solution", the observed vapor pressure is independent of whether the
Figure 3. A plot of ln[1/rt] against 1/T (K^-1).

solute is a solid or a liquid. A Clausius Clapeyron plot of the natural logarithm of 1/(corrected retention or residence time (rt_c)) as a function of 1/temperature (K^-1), results in a straight line whose slope affords the enthalpy of transfer from solution to the vapor divided by the gas constant. We have found that if the standards are chosen carefully, the enthalpy of transfer from solution to the vapor, , correlates with the vaporization enthalpies of the standards, regardless of whether the compounds are liquids or solids [6]. Figure 3 illustrates the type of correlation typically observed in ln(1/rt_c) versus 1/T plots. Enthalpies of transfer, , are listed in the second column of Table 7. A second correlation between and D
_vapH_m(298.15 K) results in Figure 4 and a least squares

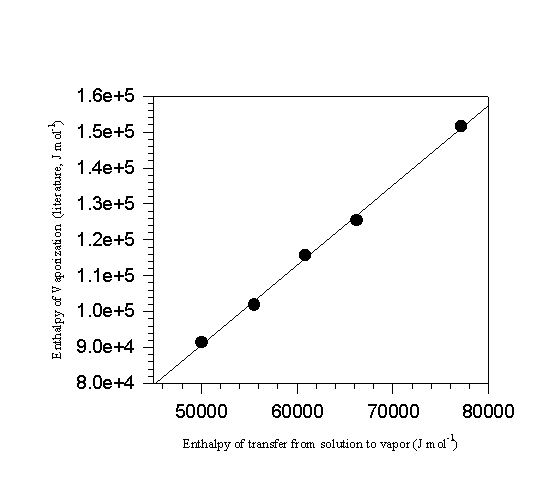Figure 4. A plot of enthalpy of vaporization against the enthalpy of transfer from solution to the vapor of the standards.

linear regression of the data produces equation 19. This equation is then used to calculate the vaporization enthalpies of each of the compounds included in the correlation, the fifth column in the table.
Table 7. Vaporization Enthalpies by Correlation Gas Chromatography

Compound

Correlation
Coefficient
r²

D_vapH_m(298.15 K)

lit^a

D_vapH_m(298.15 K)

eqn 19

octadecane

50088 ±
322

0.9999

91400

90696 ±
2730

eicosane

55504 ±
423

0.9998

101800

102755 ±
3030

docosane

60876 ±
416

0.9999

115600

114720 ±
3320

tetracosane

66289 ±
367

0.9999

125600

126772 ±
3610

octacosane

77104 ±
330

0.9999

151400

150857 ±
4200

perylene

64164 ±
438

0.9999

122040 ±
3500

coronene

75966 ±
265

0.9999

148323 ±
4140

^{areference [7]

D_vapH_m(298.15 K) = 2.23 - 20844; r² = 0.9982 (19)

3.2. VAPORIZATION ENTHALPIES OF SOLIDS BY C-GC

The protocol just described has been applied to a group of hydrocarbons and to a few hydrocarbon derivatives, all of which are solids at room temperature. The results are summarized in Table 8. Vaporization enthalpies of these materials have been measured above their melting point. The vaporization enthalpies of these materials have been adjusted to 298.15 using both equations 7 and 10 and are listed in columns 6 and 7 of the table. Vaporization enthalpies measured by correlation-gas chromatography are

Table 8. A Comparison of Vaporization Enthalpies Obtained by Gas Chromatography with Literature Values.

D_vapH_m(T_m)

[lit.]

T_m
(K)

Cp_l

Cp_g

D_vapH_m(298 K)

Eqn. 7

D_vapH_m(298 K)

Eqn. 10

D_vapH_m(298 K)

c-gc

anthracene

59390^a

519

279

219

72796

77760

79812

biphenyl

61762^b

340

249

181

64573

64910

66244

naphthalene

50246^c

371

205

151

55415

54868

53438

b
-naphthol

59697^d

416

252

154

71163

68653

77116

phenanthrene

71210^e

372

279

210

76298

77325

78650

trans stilbene

65458^f

434

304

243

73772

77640

79725

thymol

58442^f

396

291

194

67981

66893

71176

1,3,5-triphenylbenzene

116570^g

477

484

327

144676

140969

139950

^{areference [38]; ^breference [39]; ^creference [45]; ^dreference [39]; ^ereference [36, 49]; ^freference [37]; ^greference [54].

listed in the last column of the table. A comparison of the last three columns shows that the c-gc results are in good agreement with the experimental values once the experimental values are adjusted for temperature. Standard deviations of the differences between the c-gc results and equations 7 and 10 are ±
3927 and ±
3132 J mol^-1, respectively. In this case, there is no basis for identifying which equation provides the best temperature adjustment. However, the c-gc results appear to correlate better with the results of Eqn. 19

Vaporization enthalpies obtained by correlation gas chromatography for the solids in Table 8 along with some additional compounds are combined with temperature adjusted solid-liquid phase change enthalpies to obtain sublimation enthalpies at 298.15 K. These results are provided in Table 9. Heat capacity estimates for the gas phase are not available for some of the solids in Table 9 but can be estimated for the condensed phases.

3.3. SUBLIMATION ENTHALPIES BY DSC-CGC

The sublimation enthalpies in Table 9 have been calculated with the aid of equations 3 and 17 and 3 and 18 and are included in the last two columns. These values can be compared with sublimation enthalpies measured directly, column 7. It should be noted that experimental sublimation enthalpies from the literature available at temperatures other than 298.15 were corrected to 298.15 K using equation 15. Temperature adjustments to sublimation enthalpies are usually small as noted above. The standard deviation of the differences observed between columns 7 and 8 and 7 and 9 are ±
2654 and ±
2095 J mol^-1, respectively. Regardless of the protocol used, vaporization enthalpies obtained by correlation gas chromatography and combined with temperature adjusted fusion enthalpies result in sublimation enthalpies that are in good agreement with values measured directly.

3.4. SUBLIMATION ENTHALPIES OF PERYLENE AND CORONENE

There are several reports of the sublimation enthalpies of perylene and coronene in the literature. Coronene, mp 715 K, is an example of a molecule that is quite non-volatile. The results are summarized in Table 10 which include the reported sublimation enthalpies at the mean temperature of measurement and values adjusted to 298.15 K using equation 15. As indicated by the standard deviation of the mean, the

Table 9. Sublimation Enthalpies by Correlation Gas Chromatography and Differential Scanning Calorimetry

Cp_l

Cp_c

D_fusH_m(T_fus)

T_fus

D_vapH_m(298)

c-gc

D_subH_m(298)

lit.

D_subH_m(298)

Calcd.
Eqn. 3, 17

D_subH_m(298)

Calcd.
Eqn. 3, 18

acenaphthene

244

188

21462^a

366

66210

85310^b

83895

84617

azulene

205

157

17530^b

374

58191

76880^b

72079

72719

anthracene

279

209

29372^a

489

79812

100721^c

95779

99436

benzoic acid

212

149

18006^a

396

78865

89700^d

90744

92711

biphenyl

249

192

18580^a

342

66244

82030^b

82341

82821

cyclododecane

311

295

14800^g

334

63017

76400^h

77258

76155

cyclotetradecane

363

344

28870ⁱ

328

68459

92170^b

96786

95763

dimethyl oxalate

196

154

21100^k

325

53600

75200^l

73555

73680

fluorene

262

199

19578^e

388

72340

86130^b

86263

87602

naphthalene

205

157

19046^a

353

53438

72600^m

69850

70313

b
-naphthol

252

171

18790^a

394

77116

94620ⁿ

88257

91178

phenanthrene

279

209

15720^a

374

78650

91810^b

89042

90496

trans stilbene

304

235

27690^a

398

79725

102400^b

100463

102016

succinonitrile

159

138

3703^a

331

64559

69803^o

67579

67261

thymol

291

220

22010^p

342

71176

91026^o

90062

90880

1,3,5-triphenylbenzene

484

366

22928^q

446

139950

149545^q

145432

150936

triphenylmethane

395

297

21979^a

365

94552

112320^b

109958

111981

^{areference [36] ; ^breference [7]; ^csee text; ^dreference [40]; ^ereference [49]; ^freference [39]; ^greference [57]; ^hreference [58]; ⁱreference [44]; ^jreference [59]; ^kreference [43]; ^lreference [42]; ^mreference [61]; ⁿreference [62]; ^oreference [1]; ^preference [44]; ^qreference [54];

Table 10. Sublimation Enthalpies of Perylene and Coronene

Compound

D_subH_m(T_m)

J mol^-1

T_m

(K)

Cp_c

Cp_l

D_vapH_m(298)

c-gc

D_subH_m(298)

Eqn. 3, 15

Mean

D_fusH_m(T_fus)

T_fus

(K)

D_subH_m(298)

Eqn. 3, 18

Perylene

123200^a

383

270

369

126698

145200^b

298

145200

137564

139000^c

418

143941

±
8698

129600^d

415

134417

122040

32580

551

138087

Coronene

143200^a

383

288

401

146924

150122

135900^e

442

142213

±
6745

151900^d

407

156677

147000^c

473

154674

148323

19200

710

138285

^{areference [22]; ^breference [65]; ^creference [66]; ^dreference [67]; ^ereference [37].

sublimation enthalpies listed in the table for both of these materials are not known with a high degree of certainty. To determine whether correlation gas chromatography combined with differential scanning calorimetry could be useful in such circumstances, we have combined the vaporization enthalpies reported in Table 7 for perylene and coronene with the corresponding experimental fusion enthalpies according to the protocol just described. The pertinent data and results are included in columns 6, and 9-11 of Table 10. The gc-dsc results obtained for perylene are in good agreement with the mean value of 135151 ±
9265 J mol^-1reported in the table. The gc-dsc results obtained for coronene, however, are absurd. The sublimation enthalpy at 298.15 K is smaller than the corresponding vaporization enthalpy measured by correlation gas chromatography. An examination of the melting point of coronene reveals the cause. Equations 10 and 15 have been applied with some success up to temperatures in the neighborhood of 500 K [6, 7]. The use of these equations to adjust phase change enthalpies over larger temperatures ranges is expected to result in larger uncertainties and to fail at some point [5]. Even with perylene, mp 551 K, the uncertainty associated with the use of equations 10 and 15 is likely to be larger than for most compounds in Table 9. The limitations associated with the use of these equations at higher temperatures, prompted us to address this problem from a different perspective.

4 Estimation of Phase Change Entropies at 298.15 K

4.1. GROUP ADDITIVITY RELATIONSHIPS FOR HYDROCARBONS

The use of equation 18 to adjust experimental fusion enthalpies from the experimental melting point to 298.15 K suggested an alternative approach for dealing with materials that exhibit high melting points. We have previously reported a group additivity approach for estimating total phase change entropies and enthalpies associated in going from 0 K to the isotropic liquid at the melting point [8, 45]. This estimation protocol provides total phase change entropies and enthalpies at the melting point. Since equation 18 appears successful in adjusting fusion enthalpies below 500 K, our approach in this instance has been to first adjust the experimental total phase change enthalpies of our database to 298.15 K using this equation. The temperature adjusted total phase change enthalpies were then used to calculate total phase change entropies at 298.15 K and in turn the entropy was then parameterized as before [45]. This has been accomplished for hydrocarbons. The protocol used to estimate total phase change entropy and enthalpy of hydrocarbons at their melting point has been described recently [46]. The estimation of total phase change entropy and enthalpy at 298.15 K uses an identical protocol and will not described here in detail.
Our database used consisted of the fusion enthalpies of 253 hydrocarbons. Compounds with high melting points such as coronene were not included in the database. The parameterization resulted in the group values listed in columns 3 and 4 of Table 12A and B. The first two columns of this table summarize group values that can be used to

Table 12A. Group Contributions for Acyclic and Aromatic Hydrocarbons^a}

Group Values (J mol^-1 K^-1)
Aliphatic and Aromatic Carbon Groups T_fus 298.15 K
G_I G_I

primary sp³

CH₃-

A

17.6

12.7

secondary sp³

>CH_2,

B

7.1

1.31

6.4

1.48

tertiary sp³

-CH<,

C

-16.4

-8.2

quaternary sp³

>C<,

D

-34.8

-25.8

secondary sp²

=CH₂

E

17.3

9.2

tertiary sp²

=CH-

F

5.3

5.5

quaternary sp²

=CR-

G

-10.7

-1.9

tertiary sp

H-Cº

H

14.9

13.4

quaternary sp

-Cº

I

-2.8

1.6

aromatic tertiary sp²

=C_aH-

J

7.4

5.9

quaternary aromatic sp² carbon

adjacent to an sp³ atom

=C_aR-

K

-9.6

-4

peripheral quaternary aromatic sp²

carbon adjacent to an sp²atom

=C_aR-

L

-7.5

-4.9

internal quaternary aromatic sp²

carbon adjacent to an sp² atom

=C_aR-

M

-0.7

-2.2

Table 12B. Contributions of the Cyclic Hydrocarbon Portions of the Molecule

Group Values (J mol^-1 K^-1)
Cyclic Carbon Groups T_fus 298.15 K
G_IG_I

cyclic tertiary sp3

>C_cHR

N

-14.7

-9.9

cyclic quaternary sp3

>C_cR₂

O

-34.6

22.4

cyclic tertiary sp2

=C_cH-

P

-1.6

-1.6

cyclic quaternary sp2

=C_cR-

Q

-12.3

-8

cyclic quaternary sp

=C_c=; R-C_cº

R

-4.7

-3.3

^{aprimary, secondary tertiary and quaternary carbons are identified on the basis of the number of hydrogens present, 3, 2, 1, 0, respectively.
estimate the total phase change entropy of each compound at its melting point. It should
be emphasized that estimation of the total phase change enthalpy at T_fus requires this temperature as an experimental parameter. Only a hydrocarbon’s structure is necessary to estimate total phase change entropy or enthalpy at 298.15 K.
The total phase change entropy of a hydrocarbon can be estimated by using equation 20. For aromatic and acyclic hydrocarbons (aah), only the first term in equation 20, equation 21, needs to be evaluated. The estimation protocol for these two classes of molecules follows the basic principles governing group additivity relationships albeit
(total) = (aah) +(ring) + (corr) 20
(aah) = +; = 1.48 when ³
;
i ¹
CH2 otherwise = 1 21

Monocyclic Compounds

(ring) = [24] + [3.6][n-3] ; n = number of ring atoms 22

Polycyclic Compounds

(ring) = [24]N+[3.6][R-3N]; R = total number of ring atoms; N= number of rings 23

with one exception. If the number of consecutive methylene groups equals or exceeds the sum of the remaining groups in the molecule, the total contribution of the methylene groups is evaluated as the product of the number of CH₂ groups, n, their group value, , and a group coefficient of 1.48. Otherwise a value of 1.0 is used for the group coefficient. Molecules containing cyclic non-benzenoid components are evaluated using equations 22 or 23, whichever is appropriate. The total phase change entropy of the ring is evaluated on the basis of the number of rings and their size. Each carbon atom with a substitution and hybridization pattern that is different from cyclic secondary sp³ is corrected according its substitution and hybridization pattern using the correction terms given in Table 12B. Any remaining acyclic or aromatic groups attached to the ring(s) are added to these terms from Table 12A using standard group additivity procedures.
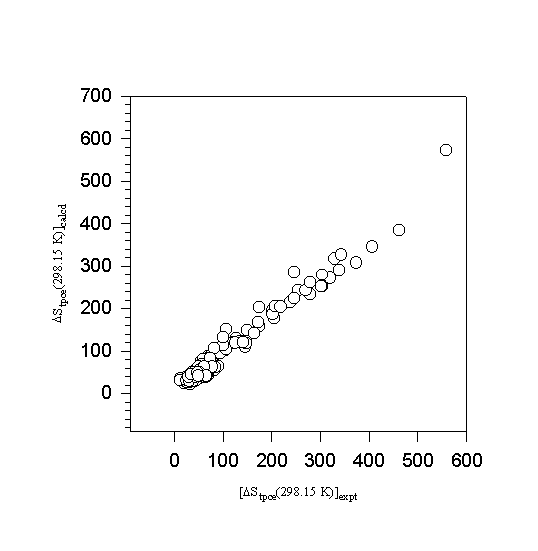
Figures 5 and 6 summarize the quality of the correlation obtained with this database. Temperature adjusted experimental and calculated total phase change entropies are plotted in Figure 5. Figure 6 illustrates the distribution of errors observed between calculated and experimental results. The standard deviation associated with differences
Figure 5. A comparison of estimated and experimental total phase change enthalpies.

between experimental and estimated total phase change entropy and enthalpy of all 253 compounds was ±
14.7 J mol^-1K^-1 and ±
4710 J mol^-1, respectively. Eliminating 8 data points characterized with errors in excess of 3 standard deviations reduced this uncertainty to ±
11.4 J mol^-1K^-1 and ±
3920 J mol^-1, respectively. The quality of this
correlation is similar to the one observed in previous estimations of D
_tpceS_m (T_fus).

4.2. SUBLIMATION ENTHALPIES USING ESTIMATED

To evaluate how well estimated total phase change enthalpies combined with vaporization enthalpies measured by correlation-gas chromatography can reproduce experimental sublimation enthalpies at 298.15 K, we have examined data for a number of

Figure 6. Error distribution in of 253 hydrocarbons

hydrocarbons. The results are shown in Table 13. The total phase change entropy and its estimation are shown in columns 2 and 3 of the table. The total phase change enthalpy at
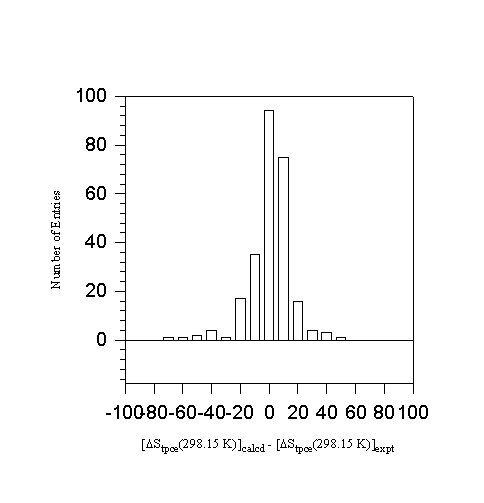298.15 K and the vaporization enthalpy measured by correlation gas chromatography are listed in columns 4 and 5. This is followed in the last two columns by the sublimation deviation of ±
6414 J mol^-1is observed in differences between the literature value and the
results calculated with the aid of equation 3.

4.3. SUBLIMATION ENTHALPIES OF PERYLENE AND CORONENE

Using the group values listed in Table 12A and 12B, it is now possible to estimate the total phase change enthalpy of perylene and coronene at 298.15 K. The results are listed in Table 14. Using the standard deviation observed in Table 13 as a guide to the accuracy of this method, a sublimation enthalpy of 133072 ±
6543 J mol^-1is obtained for perylene, in good agreement with the mean literature value of 137564 ±
8698 J mol^-1and
Table 13. Sublimation Enthalpies Calculated by Combining Fusion Enthalpies Estimated at 298.15 K with Vaporization Enthalpy Results from Correlation Gas Chromatography

Compound

J mol^-1K^-1

Estimation

J mol^-1

D_vapH_m(298)

c-gc^a

J mol^-1

D_subH_m(298)

J mol^-1
Eqn. 3

D_subH_m(298)J mol^-1

lit^a

azulene

33.6

2*33.4+4*3.6+8*P+2*Q

10018

58191

68209

76880

naphthalene

37.4

8*J+2*L

11151

53438

64589

72600

biphenyl

49.2

10*J+2*L

14669

66244

80913

82030

acenaphthene

37.7

33.4+2*3.6+3*Q+6*J+L

11240

66210

77450

85310

cyclododecane

56.4

33.4+9*3.6

16816

63017

79833

76400

fluorene

46.4

33.4+2*3.6+4*Q+8*J

13834

72340

86174

86130

anthracene

39.4

10*J+4*L

11747

79812

91559

100721

phenanthrene

39.4

10*J+4*L

11747

78650

90397

91810

trans stilbene

60.2

10*J+2*L+2*F

17949

79725

97674

102400

triphenylmethane

68.3

15*J+3*L+C

20364

94552

114916

112320

1,3,5-triphenylbenzene

76.8

18*J+6*L

22898

139950

162848

149499

cyclotetradecane

63.6

33.4+11*3.6

18962

68459

87421

92170

^{areference [6].

the value of 138087 J mol^-1obtained by combined c-gc and dsc. Similarly for coronene, the value of 156731 J mol^-1from Table 14 is in very good agreement with the last two entries in Table 10. In addition, the vaporization enthalpy measured by gas chromatography is inconsistent with the first two sublimation enthalpies reported for this compound. From the estimation in Table 14, we conclude that the sublimation enthalpy of coronene at 298.15 K is best characterized by the mean value of the last two entries of Table 9, 155500 J mol^-1. An experimental heat of formation of crystalline coronene has been published recently [63]. The reported value of 152500 ±
6900 J mol^-1, combined with a sublimation enthalpy of 155500 ±
6414 J mol^-1, results in a gas phase heat of formation of 308000 ±
9421 J mol^-1(298.15 K). Ab initio calculations by Shulman and Disch [8] predict a value of 300411 J mol^-1 while the group equivalent method of

Table 14. Estimated Sublimation Enthalpies of Perylene and Coronene

Compound

J mol^-1K^-1

Estimation

J mol^-1

D_vapH_m(298)

c-gc
J mol^-1

D_subH_m(298)

J mol^-1
Eqn. 3

perylene

37

12*J+6*L+2*M

11032

122040

133072

coronene

28.2

12*J+6*L+6*M

8408

148323

156731

Herndon [64] results in a value of 312963 J mol^-1. Both theoretical values are within the experimental uncertainty of these results. For perylene, Pedley et al. cite a value of 182800 J mol^-1for the solid. Combined with a sublimation enthalpy of 135151, this results in an enthalpy of formation at 298.15 K of 320364 J mol^-1. Herndon’s calculations result in a mean value of 332321 J mol^-1 [64].

Acknowlegement: Support from the Research Board of the University of Missouri is gratefully acknowledged.

5 References

Pedley, J. B., Naylor R. D., and Kirby, S. P. (1986) Thermochemical Data of Organic Compounds, 2^nd Edit. Chapman and Hall, N.Y.

2. Grain, C.F. (1990) Vapor Pressure in W. J. Lyman, W. F. Reehl, D. H. Rosenblatt, (eds.), Handbook of Chemical Property Estimation Methods, Amer. Chem. Soc., Washington D. C., Chapter 14.
3. Gavezzotti, A., Filippini, G. (1994) Non-Covalent Interactions in Organic Crystals, and the Calibration of Empirical Force Fields, Computational Approaches in Supramolecular Chemistry, Kluwer Academic Publishers, Dordrecht, pp 51-62.

4. Chickos J. S. "Heats of Sublimation" Chapter 2, in Molecular Structure and Energetics, Physical Measurements, Liebman J. F. and Greenberg A.; Editors; VCH Publishers, Inc; New York, 1987; Vol. 2.
5. Chickos, J. S. (1998) A Protocol for Correcting Experimental Fusion Enthalpies to 298.15 K and Its Application in Indirect Measurements of Sublimation Enthalpy at 298.15 K, Thermochim. Acta 313, 19-26.
6. Chickos, J. S., Hesse, D., Hosseine, S., Nichols, G., and Paul Webb (1998) Sublimation Enthalpies at 298.15 K Using Combined Correlation Gas Chromatography-Differential Scanning Calorimetry Measurements, Thermochim. Acta 313, 101-110.

7. Chickos, J. S. and Wilson, J. (1997) Vaporization Enthalpies at 298.15 of the n- Alkanes from C₂₁ to C₂₈ and C₃₀, J. Chem. Eng. Data 42, 190-7.
8. Schulman, J. M.; Disch, R. L. (1997) Thermal and Magnetic Properties of Coronene and Related Molecules, J. Phys. Chem. A101, 9176.
9. Domalski, E. S.; Hearing, E. D. (1988) Estimation of the thermodynamic properties of hydrocarbons at 298.15K", J. Phys. Chem. Ref. Data, 17, 1637- 1660.
10. Benson, S. W. (1976) Thermochemical Kinetics, 2^nd Ed. John Wiley and Sons:
11. Chickos, J. S., Hesse, D. G., Liebman, J. F. (1993) A Group Additivity Approach for the Estimation of Heat Capacities of Organic Liquids and Solids at 298 K, Struct. Chem. 4, 261-269.
12. Birkett, J. D. (1990) Heat Capacity in W.J. Lyman, W. F. Reehl, D. H. Rosenblatt (eds.), Handbook of Chemical Property Estimation Methods, Amer. Chem. Soc., Washington D. C.
13. Sidgwick, N. V. (1933) The Covalent Link in Chemistry, Cornell Univerity Press, Ithaca, N. Y.
14. Shaw, R. (1969) Heat Capacity (Cp) of Organic Liquids and Vapors at 25C, J. Chem. Eng. Data 14, 461.
15. Chickos, J. S., Hosseini, S., Hesse, D. G., Liebman, J. F. (1993) Heat Capacity Corrections to a Standard State: A Comparison of New and Some Literature Methods for Organic Liquids and Solids, Struct. Chem. 4, 271-277.
16. J. B. Pedley, University of Sussex, personal communication as cited by Burskinshaw, P. M., Mortimer, C. T. (1984) Enthalpies of Sublimation of Transition Metal Complexes, J. Chem. Soc., Dalton Trans. 75.
17. Melia, T. P., Merrifield, R. J. (1970) Thermal Properties of Transition Metal Compounds. Heat Capacity, Entropy, Enthalpy, Free Energy and Heat of Fusion of Scandium (III), Vanadium (III), Manganese (III), Iron (III), and Cobalt (III) and the Vapour Pressure of Tris(acetylacetonato)iron (III) Inorg. Nucl. Chem. 32, 2573.
18. DeKruif, C. G., Voogd, J., Offringa, J. C. A. J. (1979) Enthalpies of sublimation and vapour pressures of 14 amino acids and peptides, J. Chem. Thermodyn. 11, 651-6.

Majer, V., Svoboda, V. (1985) Enthalpies of Vaporization of Organic Compounds, A Critical Review and Data Compilation, IUPAC Chem. Series No. 32, Blackwell Scientific Publications, London, UK.
Hansen, P.C.; Eckert, C. A. (1986) An Improved Transpiration Method for the Measurement of Very Low Vapor Pressures, J. Chem. Eng. Data, 31, 1-3.
Adedeji, F. A.; Brown, L. S.; Connor, J. A.; Leung, M. L. Paz-Andrade I. M. Skinner, H. A. (1975) Thermochemistry of arene chromium tricarbonyls and the strengths of arene-chromium bonds. J. Organomet. Chem. 97, 221-228.
Nass, K., Lenoir, D., and Kettrup, A., (1995) Calculation of the Thermodynamic Properties of Polycyclic Aromatic Hydrocarbons by an Incremental Procedure, Angew. Chem. Int. Ed. Engl. 34, 1735.
Rordorf, B. F. (1986) Thermal Properties of Dioxins, Furans, and Related Compounds, Chemosphere 15, 1325.
Bender, R., Bieling, V., and Maurer, G. (1983) The Vapour Pressures of Solids: Anthracene, Hydroquinone, and Resorcinol", J. Chem. Thermodynamics 15, 585.
Sonnefeld, W. J., Zoller, W. H., May, W. E. (1983) Dynamic Coupled-Column Liquid Chromatographic Determination of Ambient Temperature Vapor Pressures of Polynuclear Aromatic Hydrocarbons, Anal. Chem. 55, 275.

26 De Kruif, C.G. (1980) Enthalpies of Sublimation and Vapour Pressures of 11 Polycyclic Hydrocarbons, J. Chem. Thermodynamics 12, 243.
27. Dygdala, R. S., Stefanski, K., Wolnikowski, J. (1977) Optical Determination of Anthracene Vapour Concentration, Bulletin De L’Academie Polonaise Des Sciences 15, 439-447.

Taylor, J. W.; Crookes, R. J. (1974) Vapour Pressure and Enthalpy of Sublimation of 1,3,5,7-tetranitro-1,3,5,7-tetra-azacyclooctane (HMX) J. Chem. Soc. Faraday I 723-9.

29 McEachern, D. M.; Sandoval, O. (1973) Measuring vapour pressures and heats of sublimation of organic compounds, J. Phys. E 6, 155-161.
30. Malaspina, L.; Gigli, R.; Bardi, G. (1973) Microcalorimetric determination of the enthalpy of sublimation of benzoic acid and anthracene, J. Chem. Phys. 59, 387.
31. Kelley, D.; Rice, F. (1964) The Vapor Pressures of Some Polyaromatic Hydrocarbons, J. Phys. Chem. 68, 3794.
32. Klochov, V. (1958) Saturated Vapor Pressure of Some Aromatic Compounds Zh. Fizz. Chim. 32, 1177.

Hoyer, H.; Peperle, W. Z.(1958) Dampfdruckmessungen an organischen Substanzen und ihre Sublimationswärmen, Electrochemie 62, 61.
Stevens, B. (1953) Vapour Pressures and the Heats of Sublimation of Anthracene and of 9, 10-Diphenylanthracene, J. Chem. Soc. 2973.
Bradley, R. S. Cleasby, T. G. (1953) The Vapour Pressure and Lattice Energy of Some Aromatic Ring Compounds," J. Chem. Soc. 1690.
Domalski, E. S.; Hearing, E. D. (1996) Heat Capacities and Entropies in the Condensed Phase Vol. III J. Phys. Chem. Ref. Data 25, 1-547.

37. Stephenson, R. M.; Malonowski, S. (1987) Handbook of the Thermodynamics of Organic Compounds, Elsevier, New York. Vaporization enthalpies were calculated from vapor pressures generated from the Antoine Constants reported in the text over a 30 K range followed by a Clausius Clapeyron treatment of the resulting data.
38. Nelson, O. A.; Senseman, C. E. (1922) Vapor Pressure Determinations on Naphthalene, Anthracene, Phenanthrene, and Anthraquinone between Their Melting and Boining Points, Ind. Eng. Chem. 14, 58-62.

Chirico, R. D.; Knipmeyer, A.; Nguyen, A.; Steele, W. V. (1989) The Thermodynamic Properties of Biphenyl J. Chem.Thermodyn. 21, 1307.
Cox, J. D. (1974) Recommended Reference Materials, Pure Appl. Chem. 40, 424.
DeKruif, C. G.; Van Miltenburg, J. C.; Blok, J. G. (1983) Molar heat capacities and vapour pressures of solid and liquid benzophenone, J. Chem. Thermodyn. 15, 129-136.
Chickos, J. S.; Sabbah, R.; Hosseini, S.; Liebman, J. F. (1996) The Sublimation Enthalpy of Dimethyl Oxalate, Struct. Chem. 7, 391-395.
Acree, Jr.; W. E. (1991) Thermodynamic properties of organic compounds: enthalpy of fusion and melting point compilation, Thermochim. Acta 189, 37-56.
Chickos, J. S.; Braton, C. M.; Hesse, D. G.; Liebman, J. F. (1991) Estimating Entropies and Enthalpies of Fusion, J. Org. Chem. 56, 927-938.
DeKruif, C. G.; Kuipers, T.; Van Miltenburg, J. C.; Schaake, R. C. F.; Stevens, G. (1981) The vapour pressure of solid and liquid naphthalene, J. Chem. Thermodyn. 13, 1081-1086.
Chickos, J. S., Acree, Jr. W., Liebman, J. F. (1998) Estimating Phase Change Enthalpies and Entropies in Computational Thermochemistry: Prediction and Estimation of Molecular Thermodynamics; K. K Irikura, D. J. Frurip (eds.), ACS Symp. Ser. 677; ACS, Washington DC, pp 63-91.
Piacente, V.; Ferro, D.; Della Gatta, G. (1993) Vaporization enthalpies of a series of a
, w
-alkanediols from vapour pressure measurements, Thermochim. Acta 223, 65-73.
Knauth, P.; Sabbah, R. (1990) Sublimation enthalpies of 1,w-alkanediols," Can. J. Chem. 68, 731.

Finke, H. L.; Messerly, J. F.; Lee, S. H.; Osborn, A. G.; Douslin, D. R. (1977) Comprehensive thermodynamic studies of seven aromatic hydrocarbons, J. Chem. Thermodyn. 9, 937.
Parsons, G. H.; Rochester, C. H.; Wood, C. E. C. (1971) Effects of 4-Substitution on the Thermodynamics of Hydration of Phenol and the Phenoxide Anion, J. Chem. Soc. B 533.
Wong, W. –K.; Westrum, Jr., E. F. (1971) Thermodynamics of polynuclear aromatic molecules. 1. Heat capacities and enthalpies of fusion of pyrene, fluoranthene, and triphenylene, J. Chem. Thermodyn. 3, 105-124.
Sasse, K.; Jose, J.; Merlin, J. -C. (1988) A Static Apparatus for Measurement of Low Vapor Pressures. Experimental Results on High Molecular Weight Hydrocarbons, Fluid Phase Equilibria 42, 287-304.
Sabbah, R., An, X. W. (1991) Etude Thermodynamique des Chlorobenzenes, Thermochim. Acta 179, 81-8.
Malaspina, L.; Bardi, G.; Gigli, R. (1974) Simultaneous determination by Knudsen Effusion microcalorimetric technique of the vapor pressure and enthalpy of vaporization of pyrene and 1,3,5-triphenylbenzene, J. Chem. Thermodyn. 6, 1053-1064.
Chickos, J. S.; Hosseini, S.; Hesse, D. G. (1995) Determination of vaporization enthalpies of simple organic molecules by correlations of changes in gas chromatographic net retention times, Thermochim. Acta 249, 41-62.

De Kruif, C. G.; Blok, J. G. (1982) The vapor pressure of benzoic acid, J. Chem. Thermodyn. 14, 201-206.

Drotloff, H.; Moller, M. (1987) On the phase Transitions of cycloalkanes. Thermochim. Acta 112, 57.
van Kamp, H. (1957) Energetische Grootheden van Cyclanen, Doctoral Dissertation, Vrije Universiteit: Amsterdam, The Netherlands.
Chickos, J. S.; Hesse, D. G.; Panshin, S. Y.; Rogers, D. W.; Saunders, M.; Uffer, P. M.; Liebman, J. F. (1992) The Strain Energy of Cyclotetradecane Is Small, J.Org. Chem. 57, 1897-1899.
Chickos, J. S.; Sabbah, R.; Hosseini, S.; Liebman, J. F. (1996) The Sublimation Enthalpy of Dimethyl Oxalate, Struct. Chem. 7, 391-395.
Sabbah, R. (1987) IUPAC-Recommended Reference Materials for the Realization of Physicochemical Properties, Marsh, K. N. (Ed.) Blackwell Scientific Publications: Oxford UK.
Colomina, M.; Roux, M. V.; Turrion, C. (1974) Thermochemical properties of naphthalene compounds. I. Enthalpies of combustion and formation of the 1 and 2-naphthoic acids, J. Chem. Thermodyn. 6, 149.
Kiyobayashi, T. (1995) Doctoral Thesis, Microcalorimetry Research Center, Faculty of Science, Osaka University, Toyonaka 560, Japan, 1996. Kiobayashi, T. Annual Report of the Microcalorimetry Center; 16, 58.
Herndon, W. C. (1995) Hydrocarbon Enthalpies of Formation and ab initio calculations, Chem. Phys. Lett.234, 82.
Gigli, R.; Malaspina, L.; Bardi, G. (1973) Vapor pressure and sublimation enthalpy of perylene, Ann. Chim. (Rome) 63, 627; (1995) Chem. Abstr. 82, 77775g.

66. Hoyer, H.; Peperle, W. (1958) Dampfdruckmessungen an organischen Substanzen und ihre Sublimationwärmen, Z. Electrochem. 62, 61-66.
67. Inokuchi, H.; Shiba, S. Handa, T.; Akamatu, H. (1952) Heats of Sublimation of Condensed Polynuclear Aromatic Hydrocarbons, Bull. Chem. Soc. Jpn. 25, 299-302.
68. Wakayama, N.; Inokuchi, H. (1967) Heats of Sublimation of Polycyclic Aromatic Hydrocarbons and Their Molecular Packings, Bull Chem. Soc. Jpn. 40, 2267-71.}}}}}}}

99700	383	1968	2723	101668	102423	[22]
98745	346	1102	1524	99847	100269	[23]
102600 ± 1300	338	924	1279	103524	103879	[20]
94592	376	1805	2499	96398	97091	[24]
91800 ± 3766	303	112	156	91912	91956	[25]
104500 ± 1000	298	0	0	104500	104500	[26]
104766 ± 800	383	1971	2728	106737	107494	[27]
97194 ± 1674	351	1229	1701	98423	98895	[28]
97069 ± 837	298	0	0	97069	97069	[21]
95814 ± 5858	303	112	156	95926	95969	[29]
101035 ± 460	393	2188	3028	103223	104063	[30]
99690 ± 750	393	2200	3044	101890	102734	[30]
98300 ± 560	351	1214	1680	99514	99980	[31]
100834	388	2084	2884	102918	103718	[32]
103400	338	924	1279	104324	104679	[33]
97487 ± 2090	399	2331	3225	99818	100713	[34]
92268 ± 8786	364.15	1121	2118	93799	94386	[35]
101600 ± 2050	347	1531	1552	102721	103152	[33]

Compound	D _fusH (lit)^a	T_fus	D _vapH (T_m) (lit)^b	T_m	Cp_l	Cp_c	Cp_g	D _subH_m (298) Eqn. 7,17	D _subH_m (298) Eqn. 10,18	D _subH_m (298) (lit)
anthracene	29372	489	59390^c	519	279	209	186	95778	97382	100721^d
benzoic acid	18006	396	69189^x	396	212	149	na^w	na^w	89478	89700^e
benzophenone	18194	321	73462^f	353	300	220	na^w	na^w	95263	95570^f
biphenyl	18580	342	61762^g	340	249	192	161	81528	81478	82030^p
2,4-dinitrotoluene	20120^h	343	76862	359	263	227	na^w	na^w	99806	99600^I
2-isopropyl-5-methylphenol	22010^j	324	58442	396	291	220	205	87057	87544	89264^I
naphthalene	19046	353	50246^k	371	205	157	134	71808	71727	72600^l
1,8-octanediol	36100^h	333	101100^m	356	361	262	195	143373	141001	139300ⁿ
phenanthrene	16681^a,o	372	71210^o	372	279	209	186	89576	90241	90880^p
phenol	11514	314	57375	329	177	119	102	70290	70032	69700^q
pyrene	17355^r	424	75640^s	433	295	218	203	95775	97998	100200^t
trans stilbene	27690	397	65460	434	304	235	203	100000	100018	102400^p
1,2,4,5-tetra-chlorobenzene	26340	421	52046	434	228	184	151	83417	82773	83200^u
1,3,5-triphenyl-benzene	22930^v	449	116570^v	477	484	366	327	149861	151756	149499^p

Temperature (K)	543.15	553.15	563.15	573.15	583.15
Compound			Retention (s)	Time

carbon tetrachloride	46.5	47.58	48.36	48.18	48.48
octadecane	67.62	64.98	62.7	60	58.38
eicosane	82.2	76.32	71.64	66.9	63.9
docosane	105.9	94.38	85.5	77.46	72.12
tetracosane	144.42	123.06	106.98	93.54	84.36
octacosane	306.9	239.52	191.34	154.5	129.42
perylene	348.9	283.02	232.92	192	162.9
coronene	1312.98	984.54	748.74	572.1	448.86

Compound		Correlation Coefficient r²	D_vapH_m(298.15 K) lit^a	D_vapH_m(298.15 K) eqn 19
octadecane	50088 ± 322	0.9999	91400	90696 ± 2730
eicosane	55504 ± 423	0.9998	101800	102755 ± 3030
docosane	60876 ± 416	0.9999	115600	114720 ± 3320
tetracosane	66289 ± 367	0.9999	125600	126772 ± 3610
octacosane	77104 ± 330	0.9999	151400	150857 ± 4200
perylene	64164 ± 438	0.9999		122040 ± 3500
coronene	75966 ± 265	0.9999		148323 ± 4140

	D_vapH_m(T_m) [lit.]	T_m (K)	Cp_l	Cp_g	D_vapH_m(298 K) Eqn. 7	D_vapH_m(298 K) Eqn. 10	D_vapH_m(298 K) c-gc
anthracene	59390^a	519	279	219	72796	77760	79812
biphenyl	61762^b	340	249	181	64573	64910	66244
naphthalene	50246^c	371	205	151	55415	54868	53438
b -naphthol	59697^d	416	252	154	71163	68653	77116
phenanthrene	71210^e	372	279	210	76298	77325	78650
trans stilbene	65458^f	434	304	243	73772	77640	79725
thymol	58442^f	396	291	194	67981	66893	71176
1,3,5-triphenylbenzene	116570^g	477	484	327	144676	140969	139950

	Cp_l	Cp_c	D_fusH_m(T_fus)	T_fus	D_vapH_m(298) c-gc	D_subH_m(298) lit.	D_subH_m(298) Calcd. Eqn. 3, 17	D_subH_m(298) Calcd. Eqn. 3, 18
acenaphthene	244	188	21462^a	366	66210	85310^b	83895	84617
azulene	205	157	17530^b	374	58191	76880^b	72079	72719
anthracene	279	209	29372^a	489	79812	100721^c	95779	99436
benzoic acid	212	149	18006^a	396	78865	89700^d	90744	92711
biphenyl	249	192	18580^a	342	66244	82030^b	82341	82821
cyclododecane	311	295	14800^g	334	63017	76400^h	77258	76155
cyclotetradecane	363	344	28870ⁱ	328	68459	92170^b	96786	95763
dimethyl oxalate	196	154	21100^k	325	53600	75200^l	73555	73680
fluorene	262	199	19578^e	388	72340	86130^b	86263	87602
naphthalene	205	157	19046^a	353	53438	72600^m	69850	70313
b -naphthol	252	171	18790^a	394	77116	94620ⁿ	88257	91178
phenanthrene	279	209	15720^a	374	78650	91810^b	89042	90496
trans stilbene	304	235	27690^a	398	79725	102400^b	100463	102016
succinonitrile	159	138	3703^a	331	64559	69803^o	67579	67261
thymol	291	220	22010^p	342	71176	91026^o	90062	90880
1,3,5-triphenylbenzene	484	366	22928^q	446	139950	149545^q	145432	150936
triphenylmethane	395	297	21979^a	365	94552	112320^b	109958	111981

Compound	D_subH_m(T_m) J mol^-1	T_m (K)	Cp_c	Cp_l	D_vapH_m(298) c-gc	D_subH_m(298) Eqn. 3, 15	Mean	D_fusH_m(T_fus)	T_fus (K)	D_subH_m(298) Eqn. 3, 18
Perylene	123200^a	383	270	369		126698
	145200^b	298				145200	137564
	139000^c	418				143941	± 8698
	129600^d	415				134417
					122040			32580	551	138087
Coronene	143200^a	383	288	401		146924	150122
	135900^e	442				142213	± 6745
	151900^d	407				156677
	147000^c	473				154674
					148323			19200	710	138285

primary sp³	CH₃-	A	17.6		12.7
secondary sp³	>CH_2,	B	7.1	1.31	6.4	1.48
tertiary sp³	-CH<,	C	-16.4		-8.2
quaternary sp³	>C<,	D	-34.8		-25.8
secondary sp²	=CH₂	E	17.3		9.2
tertiary sp²	=CH-	F	5.3		5.5
quaternary sp²	=CR-	G	-10.7		-1.9
tertiary sp	H-Cº	H	14.9		13.4
quaternary sp	-Cº	I	-2.8		1.6
aromatic tertiary sp²	=C_aH-	J	7.4		5.9
quaternary aromatic sp² carbon
adjacent to an sp³ atom	=C_aR-	K	-9.6		-4
peripheral quaternary aromatic sp²
carbon adjacent to an sp²atom	=C_aR-	L	-7.5		-4.9
internal quaternary aromatic sp²
carbon adjacent to an sp² atom	=C_aR-	M	-0.7		-2.2

cyclic tertiary sp3	>C_cHR	N	-14.7	-9.9
cyclic quaternary sp3	>C_cR₂	O	-34.6	22.4
cyclic tertiary sp2	=C_cH-	P	-1.6	-1.6
cyclic quaternary sp2	=C_cR-	Q	-12.3	-8
cyclic quaternary sp	=C_c=; R-C_cº	R	-4.7	-3.3

Compound	J mol^-1K^-1	Estimation	J mol^-1	D_vapH_m(298) c-gc^a J mol^-1	D_subH_m(298) J mol^-1 Eqn. 3	D_subH_m(298)J mol^-1 lit^a

azulene	33.6	233.4+43.6+8P+2Q	10018	58191	68209	76880
naphthalene	37.4	8J+2L	11151	53438	64589	72600
biphenyl	49.2	10J+2L	14669	66244	80913	82030
acenaphthene	37.7	33.4+23.6+3Q+6*J+L	11240	66210	77450	85310
cyclododecane	56.4	33.4+9*3.6	16816	63017	79833	76400
fluorene	46.4	33.4+23.6+4Q+8*J	13834	72340	86174	86130
anthracene	39.4	10J+4L	11747	79812	91559	100721
phenanthrene	39.4	10J+4L	11747	78650	90397	91810
trans stilbene	60.2	10J+2L+2*F	17949	79725	97674	102400
triphenylmethane	68.3	15J+3L+C	20364	94552	114916	112320
1,3,5-triphenylbenzene	76.8	18J+6L	22898	139950	162848	149499
cyclotetradecane	63.6	33.4+11*3.6	18962	68459	87421	92170