DES ENCRYPTION

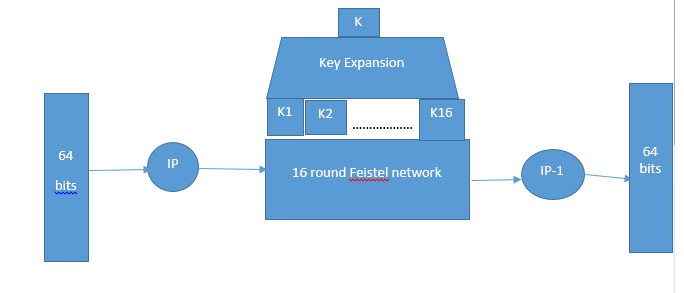
- Plainext is broken into blocks of length 64 bits.Encryption is blockwise.
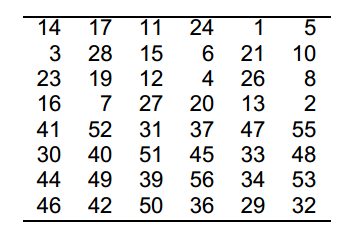
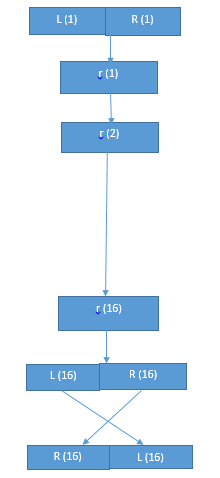
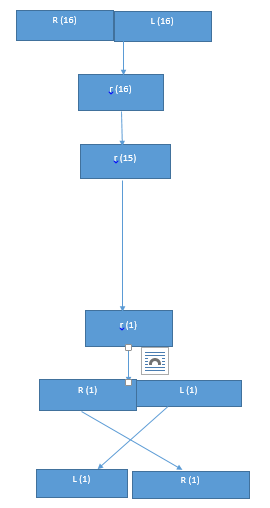
- A message block is first gone through an initial permutation IP,then divided into two parts L0,where L0 is the left part of 32 bits and R0 is the right part of the 32 bits
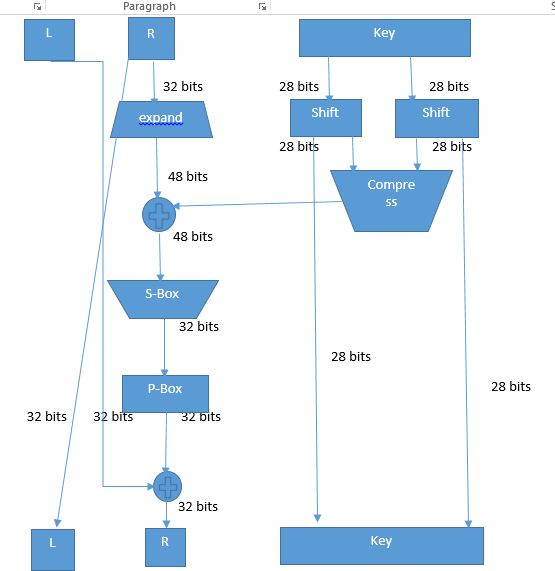
- Round i has input Li-1,Ri-1 and output Li,Ri
- Li = Ri-1,Ri = Li-1 ⊕ f(Ri-1,Ki)
- and Ki is the subkey for the 'i'th where 1 ≤ i ≤ 16
- L1 = R0, R1 = L0 ⊕ f(R0,K1)
- L2 = R1, R2 = L1 ⊕ f(R1,K2)
- L3 = R2, R3 = L2 ⊕ f(R2,K3)
- ................ ..........................
- ................ ..........................
- ................ ..........................
- L16 = R15, R16 = L15 ⊕ f(R15,K16)
- After round 16,L16 and R16 are swapped,so that the decryption algorithm has the same structure as the encrption algorithm.
- Finally,the block is gone through the inverse the permutation IP-1 and then output
- One round of DES in very simple way during encryption
DES DECRYPTION
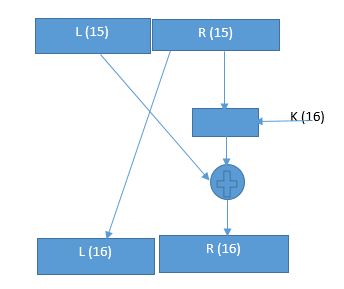
- Observation:In encryption,we have
- Li = Ri-1,Ri = Ri = Li-1 ⊕ f(Ri-1,Ki)
- and Ki is the subkey for the 'i'th round.Hence
- Ri-1 = Li,Li-1 = Ri ⊕ f(Li,Ki) for each 'i'
- Due to swap operation after the 16th round encryption,the output of encryption is IP-1(R16,L16)
- Equation(1) as follows:
- R15 = L16, L15 = R16 ⊕ f(L16,K16)
- R14 = L15, L14 = R15 ⊕ f(L15,K15)
- R13 = L14, L13 = R14 ⊕ f(L14,K14)
- ................ ..........................
- ................ ..........................
- ................ ..........................
- R1 = L2, L1 = R2 ⊕ f(L2,K2)
- If we give IP-1(R16,L16) as the input for the same algorithm with round subkeys(K16,K15,......K1),then the output is IP-1(L0,R0),the original message block
- Decryption is performed using the same algorithm,except the K16 is used as the first round,K15 in the second,and so on,with K1 used in the 16th round
- One round of DES in very simple way during decryption

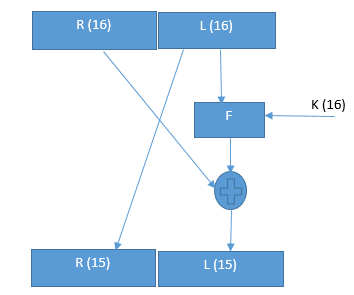
Difference between encryption and decryption in very simple way
Initial permutations
- DES has an initial permutation and final permutation after 16 rounds
- these permautations are inverse of each other and operate on 64 bits.
- They have no cryptographic significance.
- The designers did not disclose their purpose
- The initial permutation will look like this
- Input and Output of the permutation layer
- (X1,X2,......,X64)------->(XIP(1),XIP(2),-------->,XIP(64))

- The final permutation will look like this
- (X1,X2,......,X64)------->(XIP(1)-1,XIP(2)-1,-------->,XIP(64)-1)
One round of the DES
DES Expansion
- Input 32 bits
- Output 48 bits

DES S-Box(substitution box)
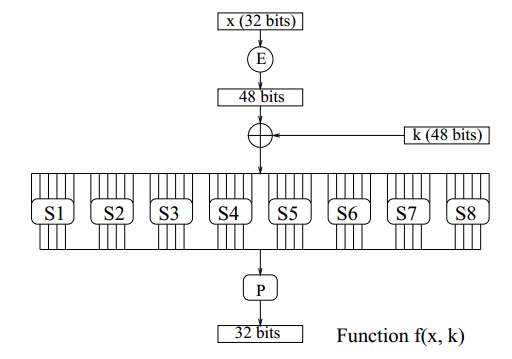
- 8 "SUbstitution boxes" or S-boxes
- Each S-box maps 6 bits to 4 bits
- S-Box(1)
- Row Index:The combination of first and last bit gives the row number
- Column Index:Remaining 4 bits gives the column number
- What is the output if input is 101000?
- Row = 10 = 2 ,Column = 0100 = 4
- we have to look at 2nd row and 4th column,then Output is 13
- here you can feel the importance of S-box.It takes 6 bits as input and gives 4 bits as output

Properties of the S-box
- There are several properties
- We highlight some:
- -The rows are permutations
- -The outputs are a non-linear combination of the inputs
- -Change one bit of the input,and half of the output bits change(Avanlanche Effect)
- -Each output bit is dependent on all the input bits
The Function f(x,k)
- This is called fiestal function or round function
- Function f is nothing but mixing of X and K
DES p-box(Permutation Box)
- Input 32 bits
- Output 32 bits
- The output bits are just Transposition of bits


DES subkey
- Input Key size:64 bits,of which 8 are parity bits
- 56 bit DES key,0,1,2,........55
Parity Check bits For Error Detection
Definition:For any binary string a1a2.........an,append another bit an+1 = a1 ⊕ a2........ ⊕ an, obtaining a1a2.........anan+1.This new sequence can detect one error

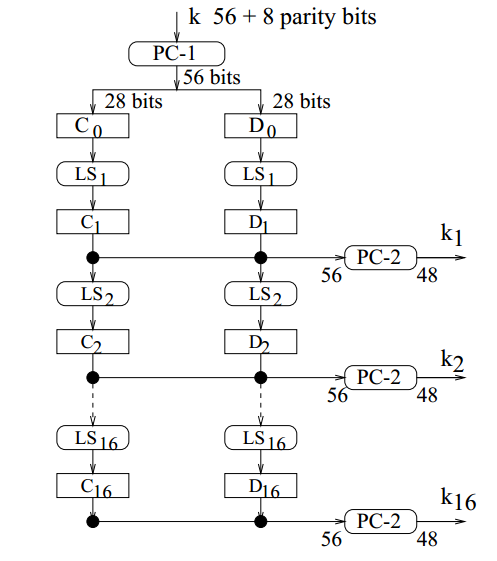
Permuted choice 1
- Key Permutation PC-1:
- with out positions 8,16,24,32,40,48,56,64 marked with "F"
- Simply given as PC-1 is a permutation of {1,2,3......,64}-{8,16,24,32,40,48,56,64}
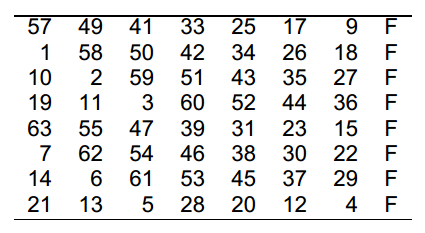
PC-1:The permutation PC-1(permuted choice 1)discards the parity bits and transposes the remaining 56 bits as below:
Left shift operation
LSi:Each LSi is a circular shift of some positions.The number of shifted positions is given below

- For rounds 1,2,9 and 16 the shifts is 1,and for the remaining all the rounds shifts are 2
- PC-2:Permuted choice 2 selects 48 bits from the 56 bit input
- PC-2
- final 48 bits obtained after the permuted choice is the Key