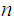 is
a five-tuple
is
a five-tuple
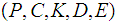 where the following conditions are satisfied:
where the following conditions are satisfied:
Working Definition: Remember that
A cryptosystem of
size 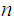 is
a five-tuple
is
a five-tuple
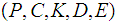 where the following conditions are satisfied:
where the following conditions are satisfied:
1.
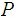 is a finite set of possible plaintexts:
is a finite set of possible plaintexts:
2.
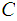 is a finite set of possible ciphertexts:
is a finite set of possible ciphertexts:
3.
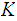 the keyspace, is the a finite set of possible
keys:
the keyspace, is the a finite set of possible
keys:
4. For each
K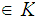 there is and encryption rule
e
there is and encryption rule
e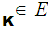 and a corresponding decryption rule
d
and a corresponding decryption rule
d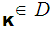 .
Where
.
Where
e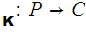 and
d
and
d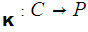 are functions such that for all
M
are functions such that for all
M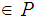 ,d
,d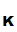 (e
(e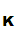 (M))
(M))
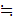 M.
M.
and
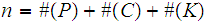
RSA ( The RSA algorithm was invented in 1978 by Ron Rivest, Adi Shamir, and Leonard Adleman):
For every pair of primes
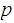 and
and
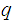 there is an "RSA" cryptosystem of size n greater than
there is an "RSA" cryptosystem of size n greater than
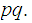
1. Next choose
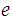 ,
,
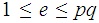 ,
such that
,
such that
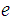 and
and
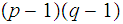 are relatively prime.
are relatively prime.
2. Using the the
Euclidean
Algorithm we can find
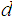 such that
such that
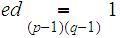 .
Note that
.
Note that
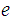 and
and
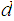 are "symmetric" for
are "symmetric" for
3. Here is RSA
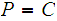 is the set of integers between
is the set of integers between
 and
and
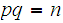 and relatively prime to
and relatively prime to
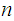 .
.
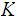 the keyspace, is the set of pairs
the keyspace, is the set of pairs
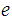 ,
,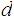 as above:
as above:
For each
K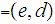 in
in
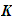 and all
M
and all
M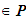 ,
e
,
e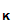 (M))
(M))
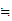 M
M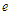 =C and
d
=C and
d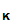 (C)
(C)
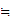 C
C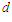
Note:
d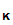 (e
(e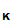 (M))
(M))
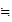 M
M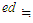 M
M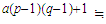 (M
(M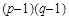 )
)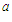 M
M (1)
(1)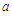 M
M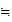 M
M
And
d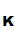 (e
(e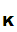 (M))=M.
(M))=M.
At first glance there may appear to be a security opening in RSA. A reasonable
question that could be asked is, while it may be hard to factor
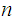 all we really need to do is find
all we really need to do is find
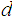 such that
such that
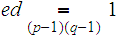 ,
so given,
,
so given,
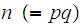 ,
is there a way to compute
,
is there a way to compute
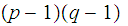 ?
?
The answer is that it is as "hard" to compute
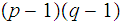 from
from
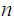 as it is to factor
as it is to factor
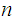 it self. Here is the argument.
it self. Here is the argument.
1. For the sake of clarity, set
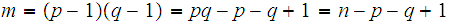 .
So if we know
.
So if we know
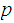 and
and
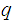 we can quickly
compute
we can quickly
compute 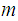 .
.
Next the important direction.
2. Suppose there was an easy way to compute
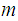 from
from
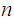 .
To factor
.
To factor
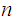 ,
we would then only have to solve the two simultaneous equations.
,
we would then only have to solve the two simultaneous equations.
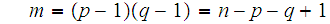
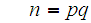
in two unknowns
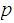 and
and
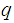 .
.
Solving the first equation for p gives.
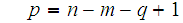
substituting this into the second equation gives.
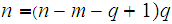
or
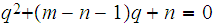 .
.
The quadratic formula does the rest.
The answer is, given
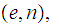 to
find
to
find
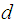 in
a timely way.
in
a timely way.