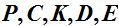 )
where the following conditions are satisfied:
)
where the following conditions are satisfied:
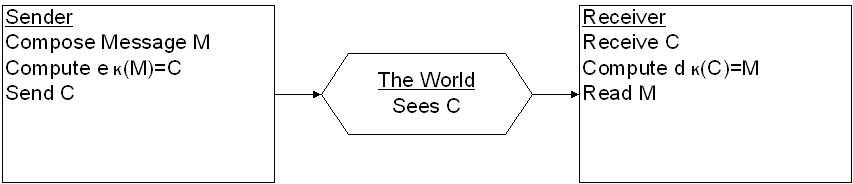
The "Key" Idea: Remember that A
cryptosystem is a five-tuple
(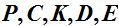 )
where the following conditions are satisfied:
)
where the following conditions are satisfied:
1.
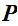 is a finite set of possible plaintexts:
is a finite set of possible plaintexts:
2.
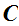 is a finite set of possible ciphertexts:
is a finite set of possible ciphertexts:
3.
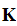 the keyspace, is the a finite set of possible
keys:
the keyspace, is the a finite set of possible
keys:
4. For each
K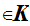 there is and encryption rule
e
there is and encryption rule
e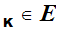 and a corresponding decryption rule
d
and a corresponding decryption rule
d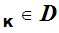 .
Where
.
Where
e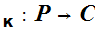 and
d
and
d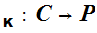 are functions such that for all
M
are functions such that for all
M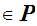 ,d
,d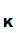 (e
(e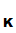 (M))
(M))
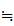 M.
M.
In general we think of cryptosystems as being used for two-way communication between individuals who want to carry on a private dialog. However, this is really not be practical for e-commerce. Consider the basic function of taking a credit card over the Web.
Suppose, however, that it were possible to find a cryptosystem for which
knowing
e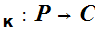 , and the general methodology used in its construction, did not lead to an
easy computation of
d
, and the general methodology used in its construction, did not lead to an
easy computation of
d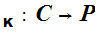 , then we could do the following.
, then we could do the following.
Secure One-Way Communication: (eg Web Form)
1. Publish
e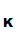 for the world to see. Tell the world that, if they want to communicate
securely with you, all they need to is apply
e
for the world to see. Tell the world that, if they want to communicate
securely with you, all they need to is apply
e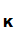 to the message before transmitting it. This because there is an acceptably
small chance of someone discovering
d
to the message before transmitting it. This because there is an acceptably
small chance of someone discovering
d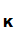 hence decoding there message.
hence decoding there message.
2. When I received the encrypted message apply
d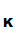 which, presumably only I know.
which, presumably only I know.
Secure Two-Way Communication:
Assume that we are dealing with a Cryptosystem such that
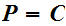
In addition to
d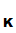 (e
(e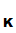 (M))
(M))
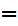 M, we have
e
M, we have
e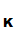 (d
(d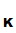 (C))
(C))
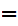 C for all
C
C for all
C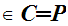 .
.
Given
d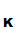 (),
it is also very hard to compute
e
(),
it is also very hard to compute
e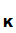 ().
().
Suppose that we have two people
P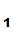 and
P
and
P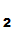 who want to communicate securely with each other. Each selects their own "one
way system",
K
who want to communicate securely with each other. Each selects their own "one
way system",
K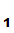 and
K
and
K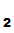 ,
from a Cryptosystem with the above listed properties .
,
from a Cryptosystem with the above listed properties .
P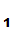 and
P
and
P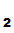 commmunicate as follows:
commmunicate as follows:
1.
P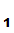 gives
e
gives
e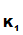 to
P
to
P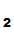 and
P
and
P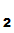 gives
e
gives
e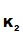 to
P
to
P .
.
2. Suppose
P wants to send message M to
P
wants to send message M to
P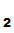 .
P
.
P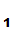 computes
C
computes
C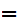 e
e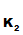 (d
(d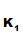 (M))
and transmits it.
(M))
and transmits it.
3.
P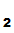 computes
e
computes
e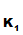 (d
(d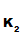 (C))
(C))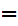 e
e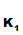 (d
(d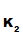 (e
(e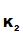 (d
(d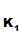 (M))))
(M))))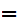 e
e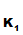 (d
(d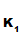 (M))
(M))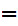 M.
M.
Why does this work?
P knows that the only person who can read the message is
P
knows that the only person who can read the message is
P , the owner of
K
, the owner of
K since, presumably
P
since, presumably
P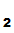 , is the only person who knows
d
, is the only person who knows
d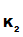 ().
().
P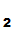 knows that
P
knows that
P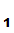 sent the message since, presumably
P
sent the message since, presumably
P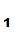 , is the only person who knows
d
, is the only person who knows
d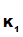 ().
We are implicitly assuming that the message
P
().
We are implicitly assuming that the message
P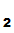
sees is meaningful.
There are Examples of One Way Cryptosystems:
RSA ( The RSA algorithm was invented in 1978 by Ron Rivest, Adi Shamir, and Leonard Adleman):
1. Begin by choosing
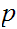 and
and
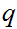 to be two very large prime numbers.
to be two very large prime numbers.
2. Next choose
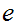 ,
,
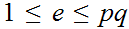 ,
such that
,
such that
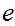 and
and
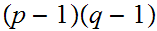 are relatively prime.
are relatively prime.
3. Referring back to the previous sections, we can find
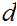 such that
such that
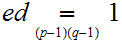 .
Note that
.
Note that
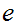 and
and
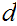 are "symmetric" for two way communication.
are "symmetric" for two way communication.
4. Here is RSA
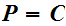 is the set of integers between
is the set of integers between
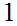 and
and
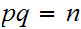 and relatively prime to
and relatively prime to
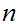 .
.
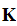 the keyspace, is the set of pairs
the keyspace, is the set of pairs
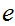 ,
,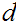 as above:
as above:
For each
K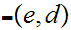 in
in
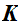 and all
M
and all
M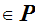 ,
e
,
e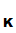 (M))
(M))
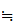 M
M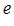 =C and
d
=C and
d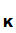 (C)
(C)
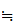 C
C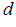
Note:
d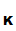 (e
(e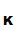 (M))
(M))
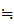 M
M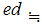 M
M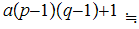 (M
(M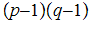 )
)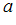 M
M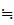 (1)
(1)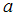 M
M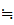 M
M
And
d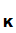 (e
(e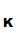 (M))=M.
(M))=M.
Example- Let
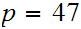 and
and
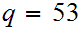 .
.
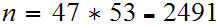
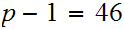 and
and
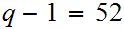 .
So
.
So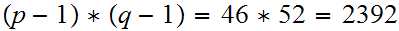 .
Choose
.
Choose
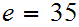 .
Note
.
Note
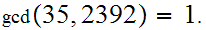
Compute
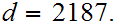
Suppose
M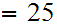
 Check
Check
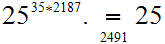
At first glance there may appear to be a security opening in RSA. A reasonable
question that could be asked is, while it may be hard to factor
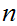 all we really need to do is find
all we really need to do is find
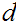 such that
such that
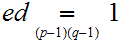 ,
so given,
,
so given,
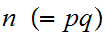 ,
is there a way to compute
,
is there a way to compute
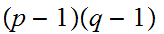 ?
?
The answer is that it is as "hard" to compute
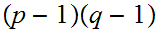 from
from
 as it is to factor
as it is to factor
 it self. Here is the argument.
it self. Here is the argument.
1. For the sake of clarity, set
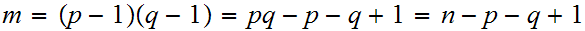 .
So if we know
.
So if we know
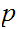 and
and
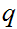 we can quickly
compute
we can quickly
compute 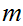 .
.
Next the important direction.
2. Suppose there was an easy way to compute
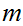 from
from
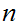 .
To factor
.
To factor
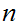 ,
we would then only have to solve the two simultaneous equations.
,
we would then only have to solve the two simultaneous equations.
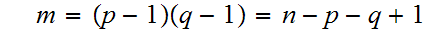
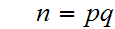
in two unknowns
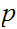 and
and
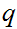 .
.
Solving the first equation for p gives.
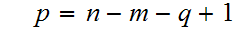
substituting this into the second equation gives.
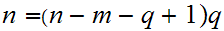
or
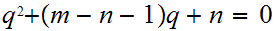 .
.
The quadratic formula does the rest.