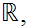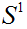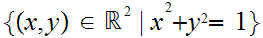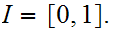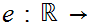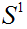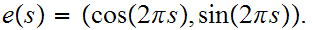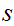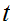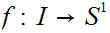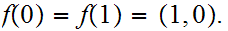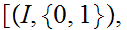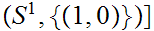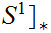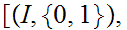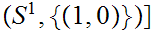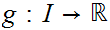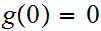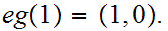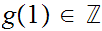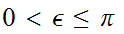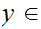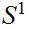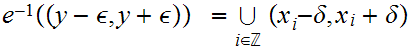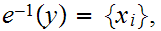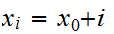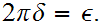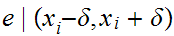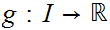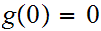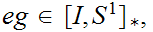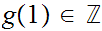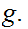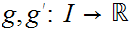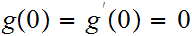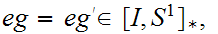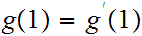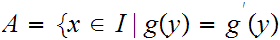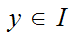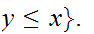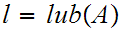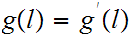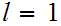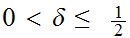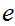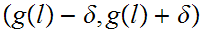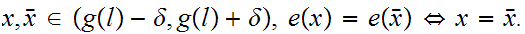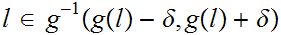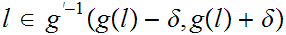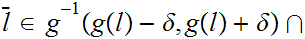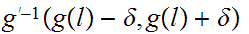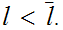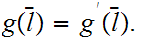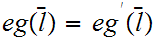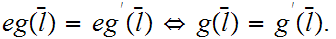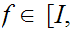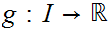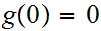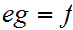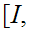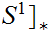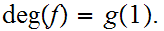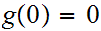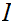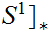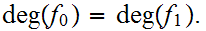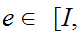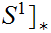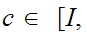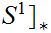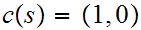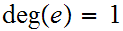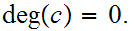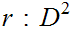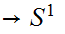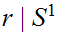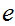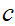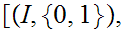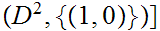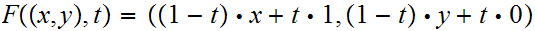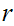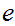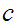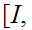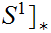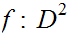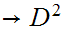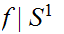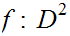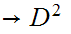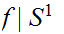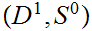The Winding Number
Definition
and Notation
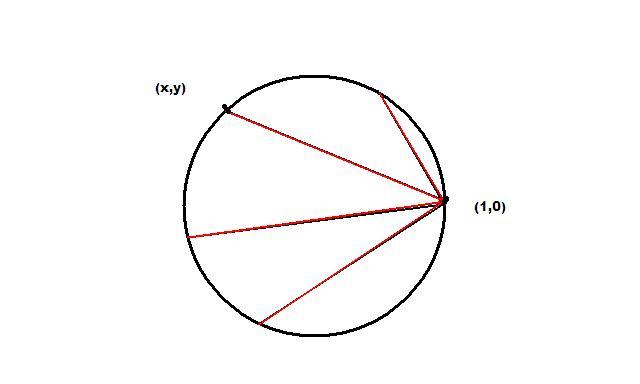
The Setting
This is the picture:
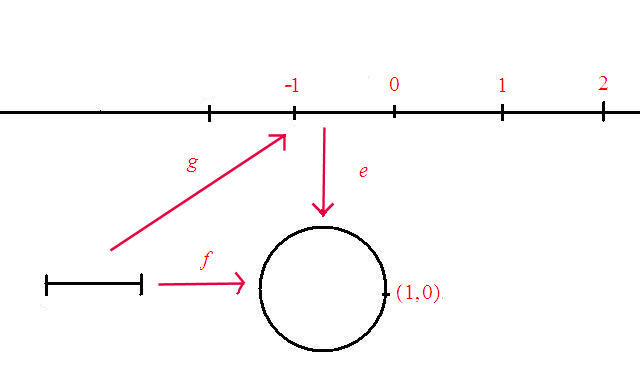
____________________________________________________________________
Lemma:
Let
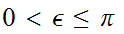 and let
and let
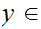
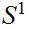 .
.
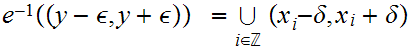
such that.
______________________________________________________________________________
Definition:
Suppose we are given a map
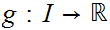 such
that
such
that
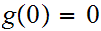 and such that
and such that
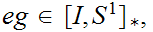 then,
then,
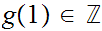 is called the winding number or degree of
is called the winding number or degree of
_____________________________________________________________________________________________________
Lemma:
Let
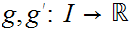 such
that
such
that
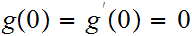 and such that
and such that
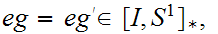 then
then
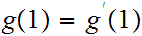
Proof:
Let
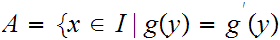 for
all
for
all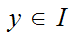 such
that
such
that
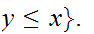 Let
Let
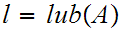 .
By the usual limit argument
.
By the usual limit argument
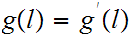 .
We want to show that
.
We want to show that
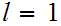 .
.
Let
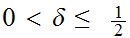 . Since
. Since
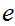 is
single-valued (in fact a homeomorphism) on
is
single-valued (in fact a homeomorphism) on
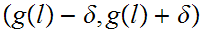 ,
for
,
for
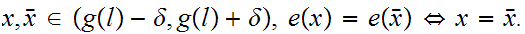
But
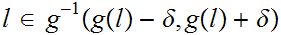 and
and
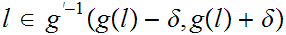 thus if
thus if
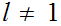 then there is
then there is
some
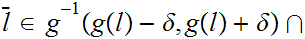
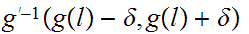 with
with
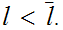
We want to show that
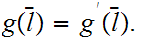 But follows from the fact that
But follows from the fact that
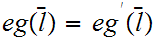 and
and
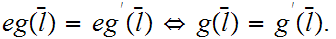
_____________________________________________________________
Lemma:
Let
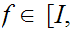
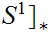 then there exists a unique
then there exists a unique
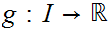 ,
such that
,
such that
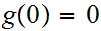 and such that
and such that
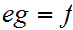 .
In particular we can define a winding number on
.
In particular we can define a winding number on
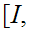
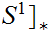 by setting
by setting
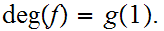
Proof:
Start with
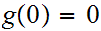 and, using the fact that
and, using the fact that
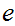 is a local homeomorphism define
is a local homeomorphism define
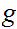 on the "largest possible" subinterval of
on the "largest possible" subinterval of
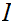 .Now
use a "lub" argument to show you can define it on all of
.Now
use a "lub" argument to show you can define it on all of
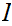 .
.
Homework due May 2. Give a detailed proof of the
lemma:
__________________________________________________________________
Theorem:
The winding number is invariant under relative homotopy. that is if
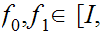
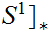 are
relatively homotopic then
are
relatively homotopic then
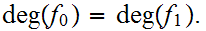
Proof(to follow)
_____________________________________________________________________________________
Consequences
-
The maps
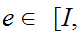
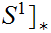 and the constant map
and the constant map
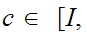
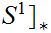 , where
, where
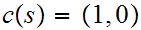 are
not relatively homotopic.
are
not relatively homotopic.
Proof:
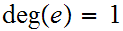 and
and
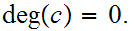
-
There does not exist a map (always read continuous)
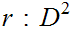
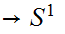 such
that
such
that
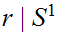 is
the identity map.
is
the identity map.
Proof:
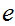 and
and
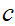 considered as maps in
considered as maps in
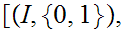
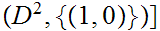 are relatively homotopic. The formula is
are relatively homotopic. The formula is
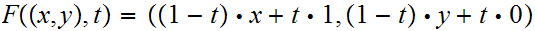
Here is the picture
composing this relative homotopy with
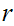 would give a relative homotopy of
would give a relative homotopy of
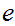 and
and
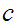 in
in
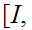
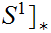 ,
contradicting 1.
,
contradicting 1.
-
Every map
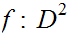
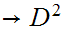 such
that
such
that
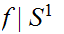 is
the identity map, is onto.
is
the identity map, is onto.
Proof: If not we could find a map contradicting
2.
-
Every map
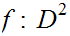
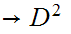 such
that
such
that
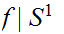 is
the identity map, has a fixed point.
is
the identity map, has a fixed point.
Proof: If not we could find a map contradicting
2.
Homework due May 2. prove 3. and 4. (hint the proofs are
almost identical to the
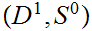 case.
case.
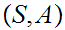 for
a pair consisting of a topological space
for
a pair consisting of a topological space
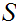 and
subspace
and
subspace
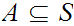 .
.
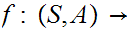
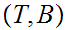 for a map
for a map
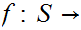
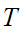 such
that
such
that
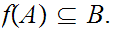
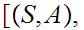
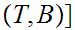 for the set of such maps.
for the set of such maps.
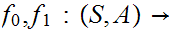
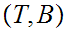 we say that
we say that
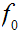 is relatively homotopic to
is relatively homotopic to
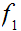 if there is a homotopy
if there is a homotopy
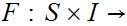
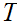 from
from
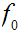 to
to
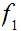 such
that
such
that
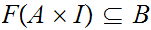 .
It is immediate that relatively homotopy is also an
equivalence relation.
.
It is immediate that relatively homotopy is also an
equivalence relation.