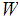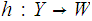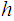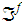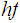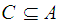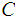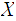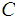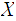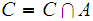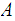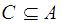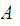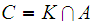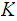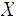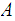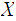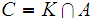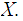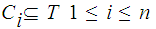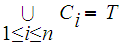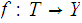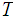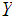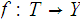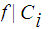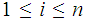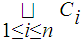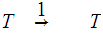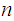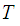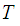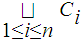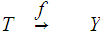Push Out Notes
Pushing out a Topology:
Given a topological space
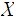 ,
a point set
,
a point set
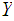 ,
and a function
,
and a function
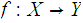 which
is onto, we define a topology on
which
is onto, we define a topology on
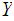 , called the quotient topology under
, called the quotient topology under
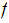 ,
to be the collection of sets
,
to be the collection of sets
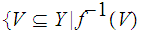 is
open in
is
open in
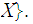 If
If
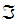 is
the given topology on
is
the given topology on
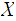 we
write
we
write
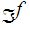 for this "pushed out " topology. That it is a topology, again, follows quickly
from the Boolean Algebra above. Moreover,
for this "pushed out " topology. That it is a topology, again, follows quickly
from the Boolean Algebra above. Moreover,
Lemma
-
Given a topological space
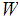 ,
and a function (set map)
,
and a function (set map)
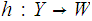 ,
then
,
then
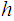 is
continuous with respect to the topology
is
continuous with respect to the topology
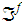 if and only if
if and only if
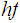 is
continuous.
is
continuous.
_______________________________________________________________
Lemma:
then
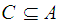 is
closed in the subspace topology if and only if
is
closed in the subspace topology if and only if
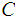 is closed in
is closed in
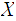 .
.
Proof:
Let
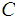 be closed in
be closed in
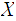 then
then
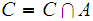 is
closed in the subspace topology of
is
closed in the subspace topology of
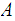 .
Let
.
Let
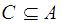 be
closed in the subspace topology of
be
closed in the subspace topology of
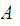 then
then
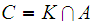 where
where
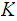 is closed in
is closed in
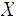 . But, by hypothesis,
. But, by hypothesis,
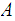 is closed in
is closed in
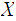 so
so
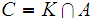 is
closed in
is
closed in
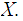
_____________________________________________________________________
Theorem (Gluing Lemma)
Let
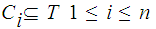 be
closed subspaces such that
be
closed subspaces such that
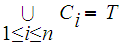 and let
and let
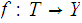 ,
be a function from
,
be a function from
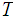 into a topological space
into a topological space
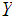 .
.
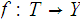 is continuous if and only if
is continuous if and only if
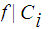 for
each
for
each
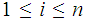 .
.
Proof:
Consider the diagram:
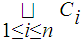

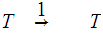
Where
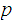 is the union of the
is the union of the
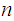 inclusions
and where the left-most
inclusions
and where the left-most
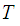 has
the push out topology and the right-most
has
the push out topology and the right-most
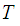 has its given topology. It is a simple argument to check that is a
homeomorphism. Use the lemma above and the fact that there is only a finite
number of closed sets.
has its given topology. It is a simple argument to check that is a
homeomorphism. Use the lemma above and the fact that there is only a finite
number of closed sets.
To prove the theorem, now consider the diagram
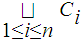

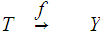
Since we can consider
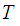 as
having the push out topology, the glueing lemma is just a restatement of the
definition of the push out topology.
as
having the push out topology, the glueing lemma is just a restatement of the
definition of the push out topology.
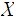 ,
a point set
,
a point set
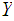 ,
and a function
,
and a function
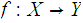 which
is onto, we define a topology on
which
is onto, we define a topology on
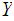 , called the quotient topology under
, called the quotient topology under
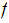 ,
to be the collection of sets
,
to be the collection of sets
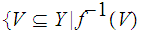 is
open in
is
open in
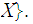 If
If
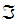 is
the given topology on
is
the given topology on
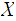 we
write
we
write
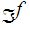 for this "pushed out " topology. That it is a topology, again, follows quickly
from the Boolean Algebra above. Moreover,
for this "pushed out " topology. That it is a topology, again, follows quickly
from the Boolean Algebra above. Moreover,