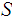 and
and
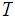 and continuous maps
and continuous maps
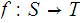 and
and
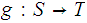 ,
we say that
,
we say that
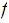 is homotopic to
is homotopic to
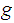 if there exists a continuous map
if there exists a continuous map
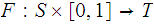 such that for all
such that for all
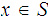 ,
,
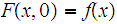 and
and
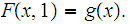
Given topological spaces
 and
and
 and continuous maps
and continuous maps
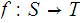 and
and
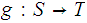 ,
we say that
,
we say that
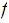 is homotopic to
is homotopic to
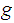 if there exists a continuous map
if there exists a continuous map
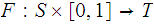 such that for all
such that for all
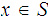 ,
,
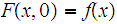 and
and
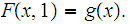
If
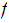 is homotopic to
is homotopic to
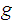 ,we use the notation
,we use the notation
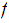
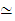
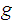
Example 1 Let
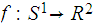 be the natural inclusion map, and let
be the natural inclusion map, and let
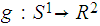 be the constant map
be the constant map
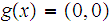 . Let
. Let
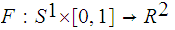 be
defined by
be
defined by
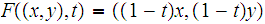 .
.
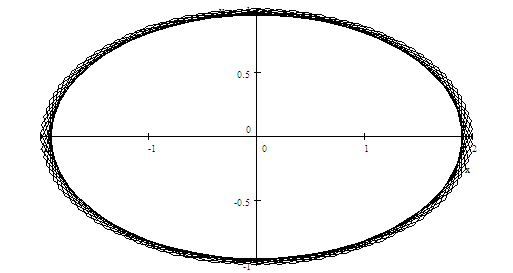
Example 2 Let
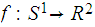
 be
the circle defined by the parametric equation ,
be
the circle defined by the parametric equation ,
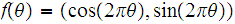
and let
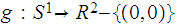 be the ellipse
be the ellipse
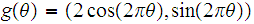 .
.
Let
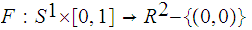 be
defined by
be
defined by
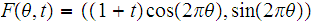
Homotopy is an equivalence relation.
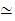
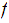 :
By the homotopy
:
By the homotopy
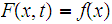
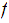
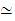
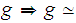
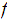 :
If
:
If
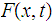 is
a homotopy from
is
a homotopy from
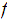 to
to
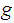 then
then
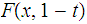 is
a homotopy from
is
a homotopy from
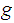 to
to
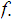
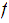
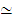
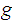 and
and
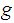
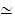
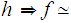
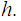
Given
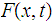 a
homotopy from
a
homotopy from
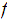 to
to
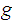 and
and
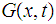 a
homotopy from
a
homotopy from
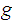 to
to
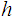 we define a function
we define a function
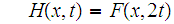 for
for
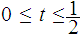
and
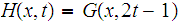 for
for
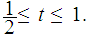
Note that this is well defined since
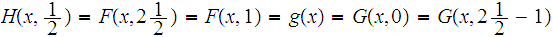
What is left to show is that the function is continuous. To do this we invoke the push out construction.
Let
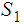 and
and
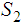 be
two topological space homeomorphic to
be
two topological space homeomorphic to
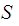 but
disjoint from
but
disjoint from
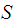 and
each other. Consider the push out diagram
and
each other. Consider the push out diagram
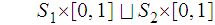
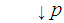
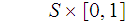
defined by
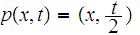 for
for
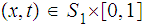
and
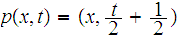 for
for
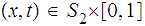
We are implicitly using the various homeomorphisms between
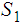 ,
, 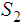 ,
and
,
and 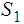
Consider the diagram:
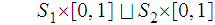
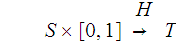
We have at once that
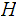 is continuous since
is continuous since
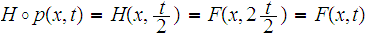 for
for
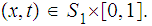
and
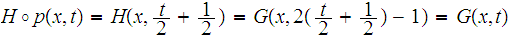 for
for
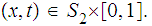
What still needs to be verified is that the identity map is a homeomorphism
between
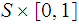 with
the push out topology and
with
the push out topology and
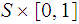 with
the product topology.
with
the product topology.
To see this we look at the diagram
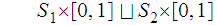
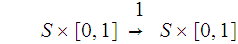
where the right most
 is considered to have the product topology. Again,
is considered to have the product topology. Again,
Homework Due Thursday April 27
verify that
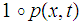 is continuous hence
is continuous hence
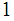 is continuous.
is continuous.
and,
under
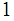 ,the
image of closed sets are closed hence the inverse of
,the
image of closed sets are closed hence the inverse of
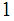 is continuous with respect to the two topologies.
is continuous with respect to the two topologies.