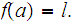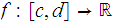 be a continuous function then
be a continuous function then
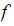 must
assume an absolute maximum value and an absolute minimum value.
must
assume an absolute maximum value and an absolute minimum value.
Let
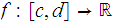 be a continuous function then
be a continuous function then
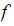 must
assume an absolute maximum value and an absolute minimum value.
must
assume an absolute maximum value and an absolute minimum value.
That
![$\QTR{Large}{[c,d]}$](graphics/extreme__3.png) is
compact is essential in the proof .
is
compact is essential in the proof .
Note:
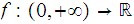 ,
where
,
where
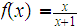 ,
assumes neither a maximum nor a minimum but is bounded above and below.
,
assumes neither a maximum nor a minimum but is bounded above and below.
We will focus on functions on the Real Line, or a closed interval on the Real Line, but we will use "Open Ball" notation to indicate that much of what we will discuss generalizes to Compact Metric Spaces.
We will write
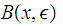 for
for
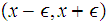 or,
in the case of a closed interval,
or,
in the case of a closed interval,
for
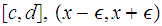
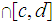
A few formalities about sequences:
A sequence in a set
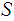 is a function
is a function
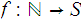 . We will denote this in the usual way as
. We will denote this in the usual way as
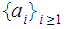
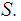
Given a function
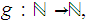 then
then
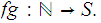 If
If
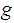 is
strictly increasing, that is
is
strictly increasing, that is
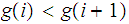 for all
for all
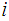 ,
then we will
,
then we will
call
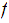
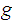 a subsequence. We will be a bit informal an just write
something like
a subsequence. We will be a bit informal an just write
something like
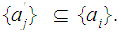
Let
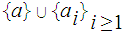
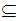
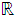 .
We write
.
We write
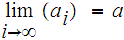 if for any
if for any
 there exists an
there exists an
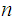 such that
such that
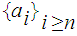
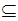
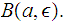 With
the same meaning we sometimes write "
With
the same meaning we sometimes write "
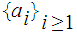 converges
to
converges
to
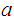 ."
."
If
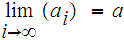 then either
then either
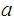 is the unique limit point of
is the unique limit point of
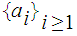 or
there exists an
or
there exists an
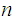 such
such
that
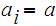 for
all
for
all
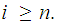
Suppose that the sequence does not become constant. That
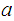 is a limit point follows from the fact that indeed all we have to show is that
at least one member of
is a limit point follows from the fact that indeed all we have to show is that
at least one member of
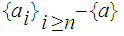 is
in
is
in
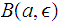 . But, in fact, we are given
. But, in fact, we are given
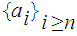
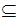
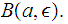 To see that the limit point is unique, let
To see that the limit point is unique, let
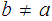 be some other point and
be some other point and
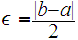 it follows from the definition of
"
it follows from the definition of
"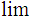 "
that
"
that
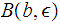 can only contain a finite number of points of
can only contain a finite number of points of
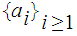 and
hence
and
hence
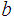 cannot
be a limit point of that set. Why?
cannot
be a limit point of that set. Why?
Show that if
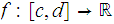 is a continuous function and
is a continuous function and
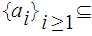
![$\QTR{Large}{[c,d]}$](graphics/extreme__54.png) is such that
is such that
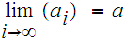 then
then
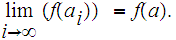
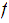 is continuous at
is continuous at
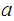 means that for any
means that for any
 there is a
there is a
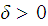 such that
such that
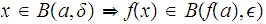
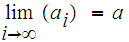 means that for any
means that for any
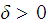 there is an
there is an
 such that
such that
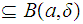
Combining these we have that for any
 there is an
there is an
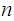 such that
such that
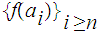
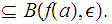
Which means
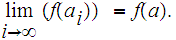
In a closed interval
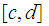 every
infinite set
every
infinite set
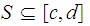 contains
a subset that can be indexed as a sequence that converges to some
contains
a subset that can be indexed as a sequence that converges to some
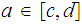 .
.
We will define a nested sequence of intervals
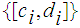 beginning with
beginning with
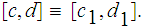
Begin by choosing any
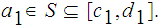 Since
Since
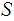 is infinite either
is infinite either
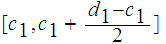 or
or
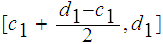 contains
an infinite subset
contains
an infinite subset
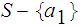 .
Letting
.
Letting
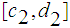 be that interval, choose
be that interval, choose
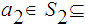
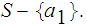
By induction we can find
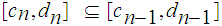 such that
such that
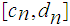 contains
an infinite subset
contains
an infinite subset
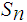
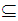
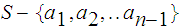 and
and
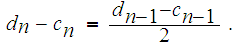 Choose
Choose
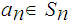 and repeat the induction step.
and repeat the induction step.
Let
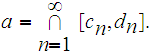 It
is straight forward to show
It
is straight forward to show
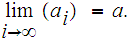 since
since
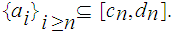
We show
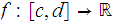 assumes an absolute maximum value. To find an absolute minimum value ,one
finds an absolute maximum of
assumes an absolute maximum value. To find an absolute minimum value ,one
finds an absolute maximum of
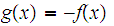 and
takes its negative.
and
takes its negative.
Let
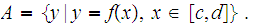 Since
we know that
Since
we know that
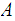 is bounded, let
is bounded, let
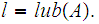
We show that there exists an
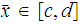 such
that
such
that
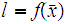 .
We know that either
.
We know that either
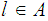 or
or
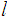 is a limit point of
is a limit point of
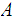 or both. To show that
or both. To show that
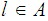 choose a sequence
choose a sequence
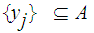 such
that
such
that
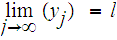 and for each
and for each
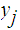 choose
choose
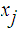
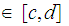 such
that
such
that
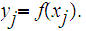 Let
Let
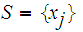 Applying
the previous Theorem we can find a subsequence
Applying
the previous Theorem we can find a subsequence
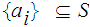 and some
and some
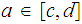 such that
such that
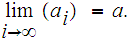 To complete the proof one shows that:
To complete the proof one shows that:
It is still the case that
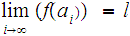
As we defined it, a subsequence of a convergent sequence is also convergent, to the the same value.
and hence by continuity
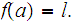
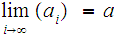
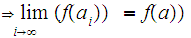 and
and
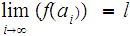 implies
implies