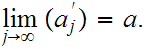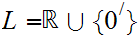 .
Define a set
.
Define a set
 to be open in
to be open in
 if:
if:
When I use a word it means exactly what I want it to mean, nothing more and nothing less.
Humpty Dumpty
from Alice in Wonderland
Let
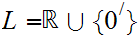 .
Define a set
.
Define a set
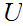 to be open in
to be open in
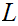 if:
if:
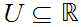 and is open in
and is open in
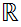 .
.
For
example,
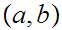
 any
any
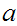 and any
and any
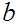 .
.
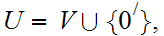
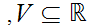 ,
,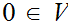 and
and
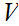 is
open in
is
open in
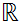 .
.
For
example,
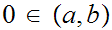
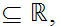 any
any
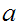 and any
and any
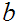 .
And
.
And
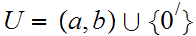
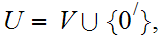
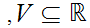 ,
,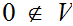 and
and
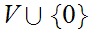 is
open in
is
open in
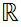 .
.
For
example,
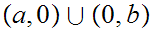
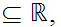 any
any
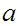 and any
and any
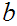 .
And
.
And
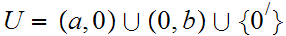
Show that this forms a topology:
 is open since
is open since
 and
and
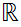 is
open in
is
open in
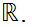
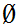 is open in
is open in
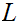 since it is open in
since it is open in
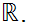
That the given subsets are closed under arbitrary unions and finite intersections follows by some simple Boolean algebra . Check that each of the three types of open sets are closed under arbitrary unions and finite intersections. Then check that a union or intersection of one set of type 1. 2. or 3. with another set of type 1. 2. or 3. gives a set of type 1. 2. or 3.
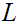 is not Hausdorff. In particular, there do not exist open sets
is not Hausdorff. In particular, there do not exist open sets
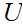 and
and
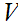 such
that
such
that
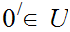 ,
,
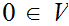 and
and
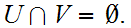
Assume
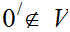 then
then
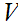 is
an open set of
is
an open set of
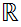 hence
for some
hence
for some
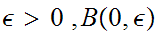
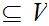 .
.
Assume
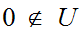 then
for some
then
for some
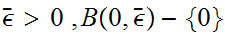
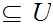
But,
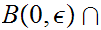
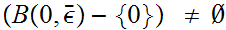
Let
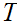 be a topological space and let
be a topological space and let
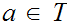 .
We can define a topology on
.
We can define a topology on
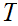 which
we write as
which
we write as
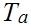 be
defining a set
be
defining a set
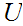 to
be open in
to
be open in
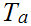 if either
if either
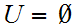 or
or
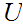 is
open in
is
open in
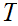 and
and
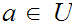 . We
call this the local topology at
. We
call this the local topology at
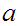 .
.
One checks that this does define a topology and if
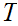 has
at least two points then it is not Hausdorff. All non-empty open sets contain
has
at least two points then it is not Hausdorff. All non-empty open sets contain
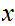 .
.
Let
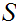 be any set. Define
be any set. Define
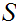 and all finite subsets to be closed. It is immediate that arbitrary
intersections and finite unions of closed sets are closed hence the
complements, the cofinite sets, and
and all finite subsets to be closed. It is immediate that arbitrary
intersections and finite unions of closed sets are closed hence the
complements, the cofinite sets, and
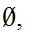 form a topology. If
form a topology. If
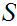 is infinite this is not Hausdorff. We want to look at the cofinite topology on
is infinite this is not Hausdorff. We want to look at the cofinite topology on
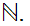
Suppose we are given
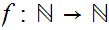 such that
such that
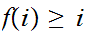 then
then
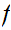 is
continuous.
is
continuous.
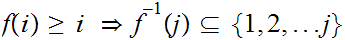 . More generally, the inverse image of finite (closed) sets are finite
(closed).
. More generally, the inverse image of finite (closed) sets are finite
(closed).
Let
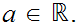 Let
Let
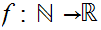 be a sequence,
be a sequence,
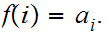
Then
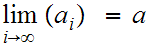 if and only if
if and only if
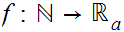 is continuous,
is continuous,
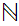 having
the cofinite topology.
having
the cofinite topology.
This is almost a trivial restatement of the various definitions.
By definition,
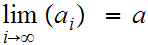 if for any
if for any
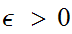 there exists an
there exists an
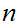 such that
such that
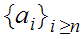
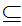
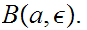
That is, the inverse image of any open set in
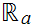 is
cofinite.
is
cofinite.
Conversely, suppose the inverse image of any open set in
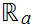 is
cofinite in
is
cofinite in
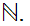 Since
Since
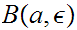 is open its inverse image is cofinite that is there exists an
is open its inverse image is cofinite that is there exists an
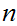 such that
such that
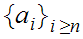
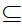
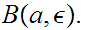
Let
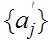 be a subsequence of a convergent sequence
be a subsequence of a convergent sequence
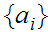 then
then
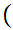
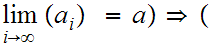
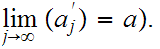
Let
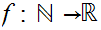 be
the functional representation of
be
the functional representation of
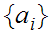 .
From the
Theorem,
.
From the
Theorem, 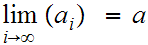 implies
implies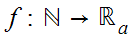 is continuous.
is continuous.
Letting
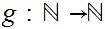 generate
the subsequence
generate
the subsequence
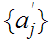 ,
,
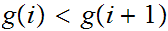 for all
for all
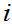 implies that
implies that
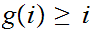
Hence
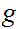 is
continuous as is
is
continuous as is
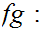
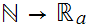 , being the composition of continuous functions. Thus, again from the Theorem,
, being the composition of continuous functions. Thus, again from the Theorem,