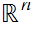 can
be described by a pair
can
be described by a pair
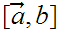 where
where
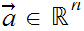 is the
"
is the
"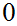 -th"
corner and
-th"
corner and
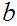
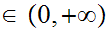 is the length of a side. For example if
is the length of a side. For example if
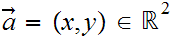 then the corners of the closed square are
then the corners of the closed square are
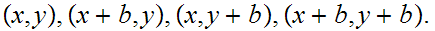
A closed n-cube in
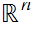 can
be described by a pair
can
be described by a pair
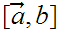 where
where
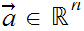 is the
"
is the
"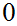 -th"
corner and
-th"
corner and
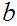
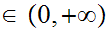 is the length of a side. For example if
is the length of a side. For example if
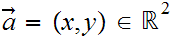 then the corners of the closed square are
then the corners of the closed square are
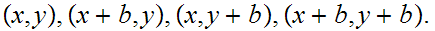
Using this notation, one can define a subdivision process that corresponds to bisecting and interval. Below, we only give the details for the square.
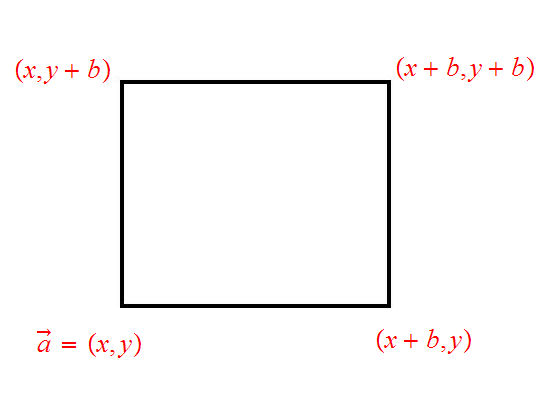
Given a closed square
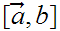 in
in
 we can subdivide it into 4 closed squares of area
we can subdivide it into 4 closed squares of area
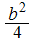 .
In our notation the squares are:
.
In our notation the squares are:
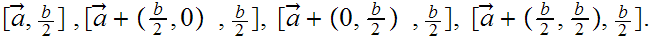
In the obvious way, one can also define a notion of a closed square
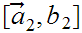 nested in a closed square
nested in a closed square
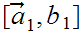 .
Note that each of the subsquares
.
Note that each of the subsquares
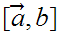 in
1. of are nested in
in
1. of are nested in
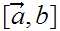 .
.
Let
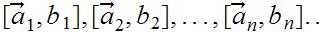 be an countable sequence of nested closed squares, then
be an countable sequence of nested closed squares, then
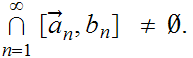
If
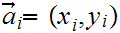 one argues that we have sequences
one argues that we have sequences
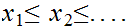
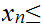 ...
... bounded
above by
bounded
above by
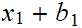
and
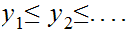
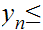 ... ...
... ... bounded
above by
bounded
above by
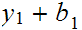
Hence each sequence has a least upper bound.
Letting
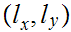 be the pair. One argues as before that
be the pair. One argues as before that
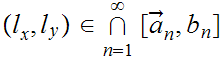 since all the squares are closed sets.
since all the squares are closed sets.