To show a specific function is continuous; If there is a metric use it in an
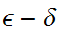 argument.
argument.
To show a general property of continuous functions; Use an Open Sets/Boolean Algebra argument, often even if it is about Metric Space.
To show a specific function is continuous; If there is a metric use it in an
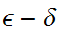 argument.
argument.
To show a general property of continuous functions; Use an Open Sets/Boolean Algebra argument, often even if it is about Metric Space.
Consider problem 2.7,
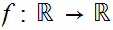 was given by the formula
was given by the formula
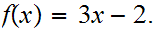
You were asked to show it was continuous by an
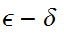 argument,
and then by showing that the preimage of every set was open.
argument,
and then by showing that the preimage of every set was open.
Given that you calculated a
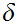 for every
for every
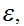 completing part one. How does the rest of the argument go?
completing part one. How does the rest of the argument go?
Let
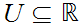 be an open set. We need to show the
be an open set. We need to show the
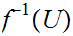 is open. Let
is open. Let
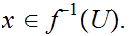 Since is open we can find some
Since is open we can find some
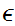 such
that
such
that
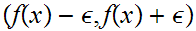
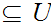 .
By the
.
By the
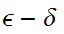 argument
we know that we can find such that
argument
we know that we can find such that
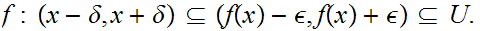 Hence
Hence
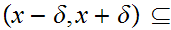
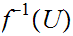 .
.
In particular, we proved part 2 by refering back to the proof in part 1.
Consider problem 3.4,
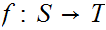 was such that the preimage of every closed set was closed. You were asked to
show that
was such that the preimage of every closed set was closed. You were asked to
show that
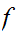 was
continuous.
was
continuous.
The proof involves some set-theoretic formulii from the "Background" notes.
If
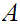 and
and
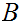 are sets, there is some algebra associated with maps (
functions) from
are sets, there is some algebra associated with maps (
functions) from
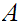 to
to
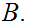
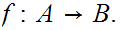
Let
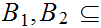
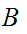 be
two subsets of
be
two subsets of
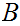 then
then
 1.
1.
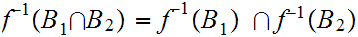
 2.
2.
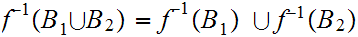
In particular, if
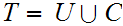 such that
such that
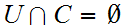 then
then
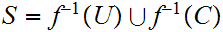 such that
such that
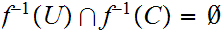
Thus if
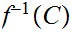 is
closed
,
is
closed
,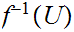 is open.
is open.
Really, the only tool we have at the moment is to show that the complement is
open. Remember, showing a set is not open does not mean that it is closed.
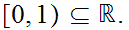
Problem 2.3 asked you to show that
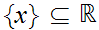 was closed for any number
was closed for any number
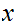 .
To do this you need to show
.
To do this you need to show
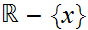 is
open.
is
open.
Thus for any
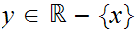 you need to find a
you need to find a
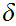 such
that
such
that
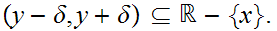 Anything
Anything
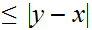 will do.
will do.