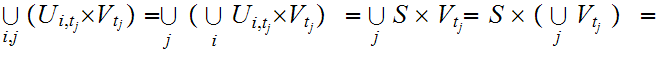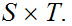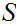 and
and
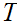 ,
a basis for the product topology on
,
a basis for the product topology on
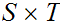 is given by all sets of the form
is given by all sets of the form
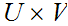 ,
where
,
where
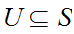 ,
and
,
and
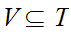 are open sets.
are open sets.
Given topological spaces
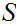 and
and
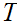 ,
a basis for the product topology on
,
a basis for the product topology on
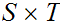 is given by all sets of the form
is given by all sets of the form
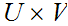 ,
where
,
where
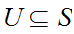 ,
and
,
and
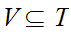 are open sets.
are open sets.
Note that the sets
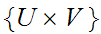 form a basis since
form a basis since
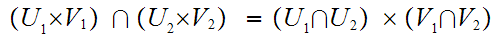 so
the sets are in fact closed under finite intersections.
so
the sets are in fact closed under finite intersections.
Given topological spaces
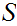 and
and
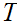 ,
, let
,
, let
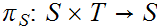 and
and
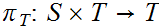 be
the projection functions (i.e.
be
the projection functions (i.e.
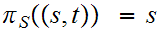 ) The product topology on
) The product topology on
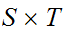 can
also be described as the topology generated by all sets of the form
can
also be described as the topology generated by all sets of the form
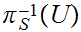 ,
or
,
or
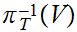 where
where
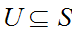 ,
and
,
and
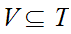 are open sets. By generated we mean "take arbitrary unions of finite
intersections of such sets."
are open sets. By generated we mean "take arbitrary unions of finite
intersections of such sets."
Note that:
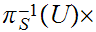
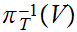
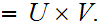
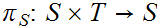 and
and
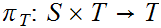 are
continuous with respect to this topology, essentially by definition.
are
continuous with respect to this topology, essentially by definition.
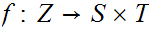 is continuous if and only if
is continuous if and only if
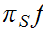 and
and
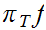 are
continuous.
are
continuous.
Due: Thursday 20
Given a topological space
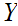 ,
a point set
,
a point set
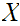 ,
and a function
,
and a function
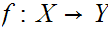 ,
show that the collection of sets
,
show that the collection of sets
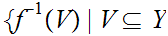 ,
,
 any
open set
any
open set
 forms a topology on
forms a topology on
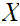 such that
such that
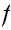 is
continuous. (see the definition of a Quotient Space)
is
continuous. (see the definition of a Quotient Space)
Given two topological spaces
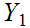 and
and
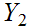 ,
a point set
,
a point set
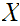 ,
and two function
,
and two function
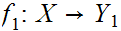 and
and
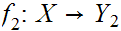 , show that the collection of sets
, show that the collection of sets
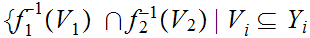 ,
,
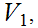
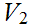 any
open
sets
any
open
sets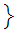 are a basis for a topology on
are a basis for a topology on
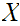 such that
such that
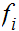 is
continuous
is
continuous
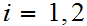 .
.
Let
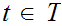 then
then
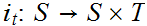 is
continuous, where
is
continuous, where
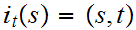 .
Similarly for
.
Similarly for
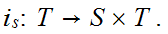
We need only show that the inverse image of basis elements are open. But
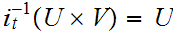 or
or
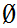 depending on whether or not
depending on whether or not
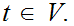
If
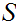 and
and
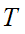 be
two compact topological spaces then
be
two compact topological spaces then
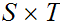 is
compact.
is
compact.
In general, since any open set is the union of basis elements it suffices to show that any open covering by basis elements admits a finite subcovering. (WHY?)
Let
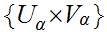 be an open covering of
be an open covering of
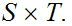 Since
Since
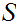 is compact and
is compact and
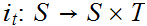 is
continuous, for each
is
continuous, for each
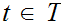 ,
we can select a finite subset
,
we can select a finite subset
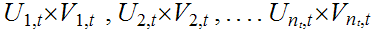 such that
such that
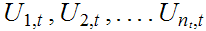 covers
covers
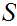 .
.
Let
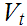
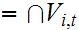 .
.
Note: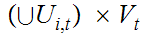
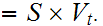
Next, since
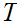 is compact, there is a finite subset
is compact, there is a finite subset
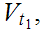
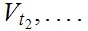
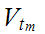 of
the
of
the
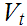 that covers
that covers
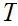 .
Thus
.
Thus
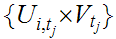 covers
covers
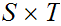 ,
as does
,
as does
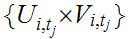 since
since
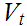
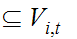 for
each
for
each
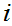 .
.