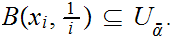Given a compact Metric Space
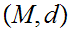 and a covering
and a covering
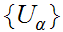 by open sets, there exists a real number
by open sets, there exists a real number
 such that every open ball of radius
such that every open ball of radius
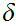 is contained in some element of
is contained in some element of
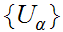 .
The number
.
The number
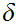 is called a Lebesgue number for the covering.
is called a Lebesgue number for the covering.
Proof:
Suppose that no Lebesgue number existed. Then there exists an open cover
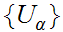 such that for all
such that for all
 there exists an
there exists an
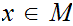 such that
no
such that
no 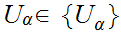 contains
contains 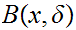 . In
particular for each
. In
particular for each
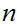 we can choose a sequence
we can choose a sequence
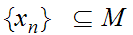 such
that
such
that
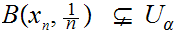 for
any
for
any
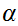 .
.
Since
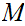 is compact choose a convergent subsequence
is compact choose a convergent subsequence
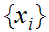 with
with
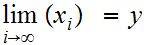 for some
for some
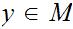 .
Since
.
Since
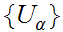 is an open cover, we know there is some
is an open cover, we know there is some
 and some
and some
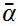 with
with
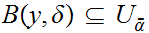 .
Again, as before, choose n such that
.
Again, as before, choose n such that
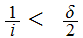 and
and
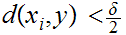 for
i
for
i 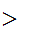 n.
Check that
n.
Check that