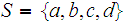 form topologies.
form topologies.
Which of the following lists of subsets of the set
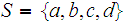 form topologies.
form topologies.
-
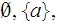
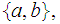
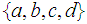 - Yes
- Yes
-
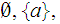
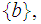
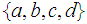 - No
- No
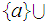
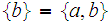 not in the list.
not in the list.
-
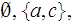
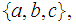
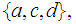
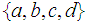 Yes
Yes
-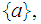
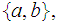
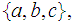
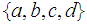 No , closed under union and intersection and
No , closed under union and intersection and
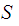 is
in the list, but
is
in the list, but
 is
not.
is
not.
Prove that a function
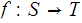 is continuous if and only if the inverse image of every closed set is closed.
is continuous if and only if the inverse image of every closed set is closed.
Proof:
We use the following equations from the Boolean algebra of sets.
If
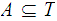 is any subset. then
is any subset. then
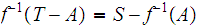
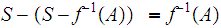
Suppose the inverse image of every closed set is closed. Let
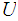 be an open set and
be an open set and
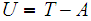
Then
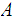 is closed and so
is closed and so
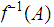 is closed hence
is closed hence
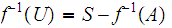 is
open.
is
open.
Suppose that
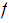 is
continuous and
is
continuous and
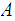 is closed then
is closed then
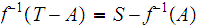 is
open since
is
open since
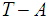 is
open
is
open
but then
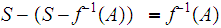 is closed.
is closed.
Let
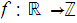 be the floor function.
be the floor function.
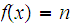 for
for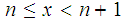
Is
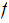 continuous?
continuous?
Answer:
No because the supspace topology on
 is descrete so points are open sets but
is descrete so points are open sets but
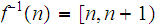
not an open set.
Let
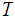 be a set and
be a set and
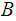 a collection of subsets closed under finite intersection, then
a collection of subsets closed under finite intersection, then
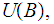 the set of arbitrary unions of sets of
the set of arbitrary unions of sets of
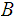 form a topology.on
form a topology.on
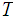 [ Added :
[ Added :
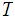 and
and
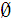 are
in
are
in
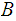 ]
]
Proof:
Again, the solution amounts to recalling some properties of Boolean Algebras. In this case
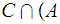
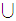
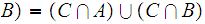
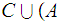
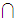
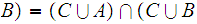
More generally, if
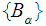 and are
and are
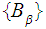 indexed
set of sets then
indexed
set of sets then
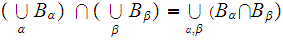
and similarly for any arbitrary collection of indexed sets.
And if
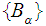 and are
and are
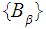 indexed
set of sets then
indexed
set of sets then
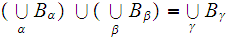 where
where
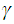 is
either in the index set
is
either in the index set
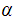 or in the index set
or in the index set
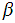 and
similarly for an arbitrary collections of index sets.
and
similarly for an arbitrary collections of index sets.
We are given that
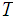 and
and
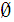 are
in
are
in
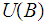 .
We are also given that arbitrary unions of sets of
.
We are also given that arbitrary unions of sets of
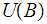 is in
is in
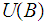 .
This is because a union of unions of sets in
.
This is because a union of unions of sets in
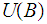 is
a union of sets. That a finit intersection of sets of
is
a union of sets. That a finit intersection of sets of
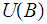 is in
is in
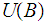 is because an intersection of unions of sets in
is because an intersection of unions of sets in
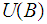 is
a union of intersections of sets.
is
a union of intersections of sets.