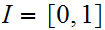
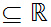 be
the unit interval, with the Subspace Topology. Let
be
the unit interval, with the Subspace Topology. Let
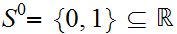 also have the Subspace Topology.
also have the Subspace Topology.
Let
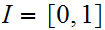
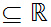 be
the unit interval, with the Subspace Topology. Let
be
the unit interval, with the Subspace Topology. Let
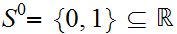 also have the Subspace Topology.
also have the Subspace Topology.
There does not exist a continuous function
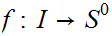 such that
such that
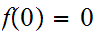 and
and
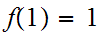 .
.
Proof:
Let
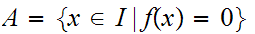 . Let
. Let
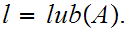 Since
Since
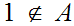 we know
we know
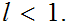 We
also know that
We
also know that
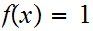 for
for

Suppose
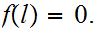
Then
since
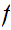 is continuous there exists a
is continuous there exists a
 such
that
such
that
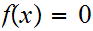 for all
for all
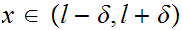 contradiction the
contradiction the
previous statement.
Hence
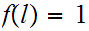 .
.
Therefore
there exists a
 such
that
such
that
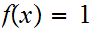 for all
for all
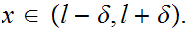
But since
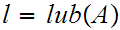 for
any
for
any
 there exists an
there exists an
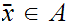 such that
such that
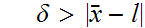 .
In particular
.
In particular
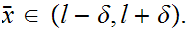 But
But
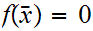 ,
again a contradiction.
,
again a contradiction.
Proving that such an
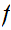 does not exist.
does not exist.
There does not exist a continuous, onto, function
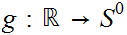 .
.
Proof:
Choose
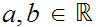 such
that
such
that
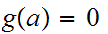 and
and
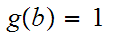 .
Define
.
Define
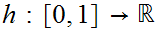 by the formula
by the formula
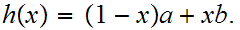 Then
Then
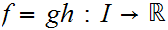 would be a continuous function
would be a continuous function
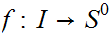 such that
such that
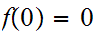 and
and
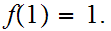 Such
functions were shown not to exist in the Theorem above.
Such
functions were shown not to exist in the Theorem above.
Let
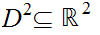 be
the unit
disk,
be
the unit
disk,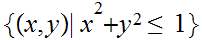 . Let
. Let
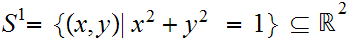 be the unit circle.
be the unit circle.
There does not exist a continuous function
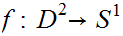 such that
such that
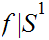 is the identity map,
is the identity map,
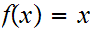 for
for
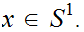
1. Let
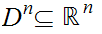 be
the unit disk, . Let
be
the unit disk, . Let
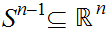 be the unit sphere.
be the unit sphere.
There does not exist a continuous function
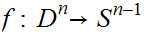 such that
such that
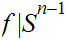 is the identity map.
is the identity map.
2. Every polynomial with complex coefficients has a complex root.