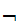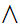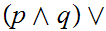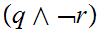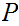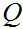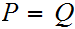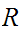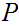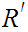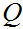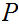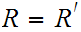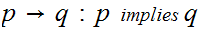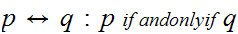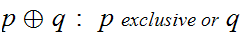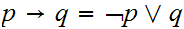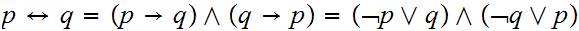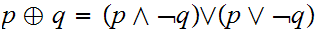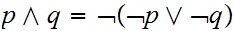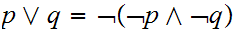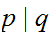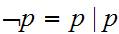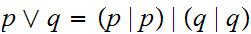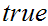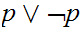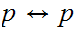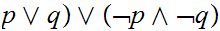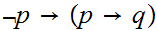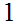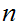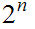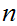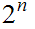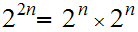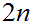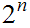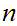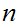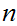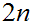0.3 Boolean Logic
0.3.1
Definition
Here is an alternative, recursive, definition of Boolean Logic:
-
The two Boolean constants are
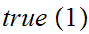 or
or
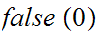 .
.
-
Boolean variables
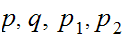 etc,can take on the values
etc,can take on the values
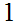 or
or
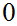 .
.
-
Boolean constants and Boolean variables are Boolean expressions.
-
If
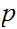 and
and
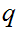 are Boolean expressions, then
are Boolean expressions, then
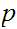
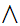
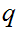 is a Boolean expression, whose truth table is
is a Boolean expression, whose truth table is
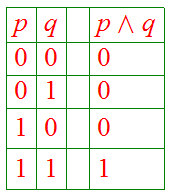
.
-
If
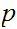 and
and
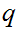 are Boolean expressions, then
are Boolean expressions, then
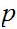
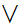
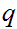 is a Boolean expression, whose truth table is
is a Boolean expression, whose truth table is
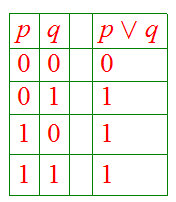
.
-
If
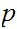 is a Boolean expressions, then
is a Boolean expressions, then
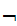
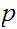 is a Boolean expression, whose truth table is
is a Boolean expression, whose truth table is
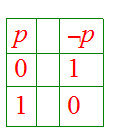
.
In forming complex Boolean expressions, the precedence levels of logical
operators is:
-
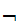
-
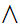
-

0.3.2 The Truth Table of Complex Boolean Expressions:
Using
4-6 above, we itteratively compute the Truth Tables of
any Boolean expression. As an example, consider
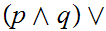
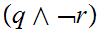

We call two Boolean
expressions ,
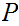 and
and
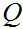 "equal"
, written
"equal"
, written
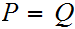 ,
if they have the sameTruth Tables.
,
if they have the sameTruth Tables.
One should check that if
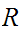 is
a Boolean expression containing
is
a Boolean expression containing
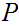 and
is
and
is
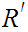 the
Boolean expression that is the result of substituting
the
Boolean expression that is the result of substituting
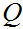 for every occurrence of
for every occurrence of
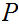 then
then
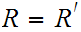 .
.
0.3.3 The Completeness of Boolean Operations
The example in 1.3.2 be though of a special case of
the following:
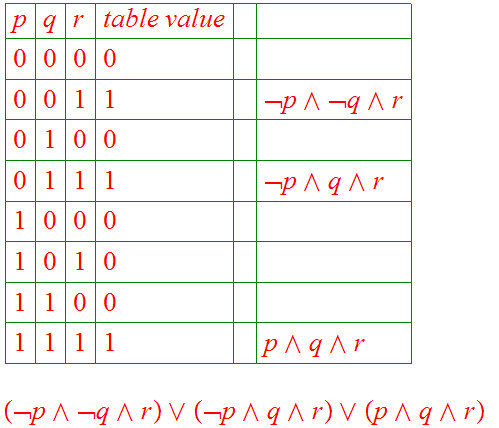
0.3.4 Theorem
Any truth table is the truth table of a Boolean expression that is the sum of
products or product of sums of Boolean variables and their negations.
Indeed we make do with negation and sum, or negation and product.
(See1.3.5 below)
Here is an example that easily generalizes
0.3.5 Derived Boolean Operations
There are a number of important Boolean expressions that are representated by
their own operation symbol. We will particularly want the following three:
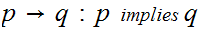
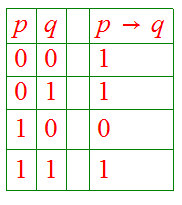
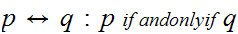
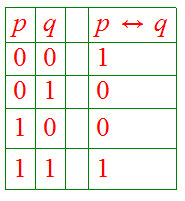
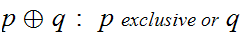
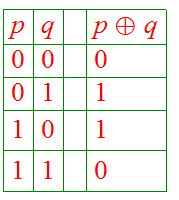
Note that, amongst others:
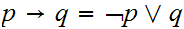
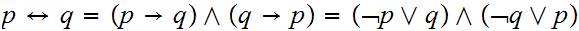
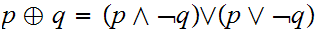
Finally, as promised in 2.4
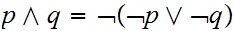
and
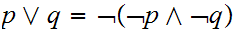
In point of fact, we can make do with the single Boolean operator
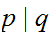 ,
the "Sheffer stroke."
,
the "Sheffer stroke."
Here is its truth table:
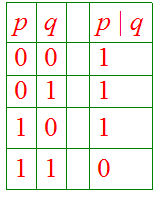
Check that:
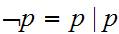
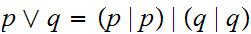
0.3.6 Tautologies
A tautology is a Boolean expression that is always
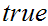 ,
that is its truth table contains only in the result column.
,
that is its truth table contains only in the result column.
Examples of tautologies:
Tautologies and proofs are
closely related concepts in Boolean logic.
0.3.7 The Tautology Problem
The question as to whether or not a given logical expression is a tautology
known as the "tautology problem."
Formally, the tautology problem is solvable in that we need only construct the
truth table for a given Boolean expression. If the result column is all
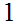 's
then the expression is a tautology.
's
then the expression is a tautology.
The more interesting question is how hard (in the computational work sense )
it is to solve the problem. If a Boolean expression has
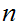 propositional variables then the corresponding truth table has
propositional variables then the corresponding truth table has
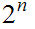 rows.
Hence, roughly, a Boolean expression with
rows.
Hence, roughly, a Boolean expression with
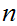 propositional variables requires
propositional variables requires
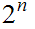 computations
to determine whether or not it is tautology.
computations
to determine whether or not it is tautology.
The associate arithmetic work is as follows:
Since
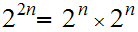 , the work associated with the
, the work associated with the
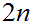 variable tautology problem is
variable tautology problem is
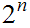 times
the work associated with the
times
the work associated with the
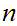 variable tautology problem. Thus, assuming that the
variable tautology problem. Thus, assuming that the
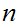 variable tautology problem is the present "practical" limit of computers, it
would require
variable tautology problem is the present "practical" limit of computers, it
would require
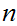 Moore Cycles to develop a computer capable of solving the
Moore Cycles to develop a computer capable of solving the
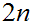 variable tautology problem.
variable tautology problem.
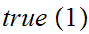 or
or
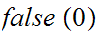 .
.
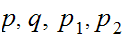 etc,can take on the values
etc,can take on the values
 or
or
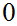 .
.
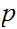 and
and
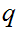 are Boolean expressions, then
are Boolean expressions, then
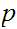
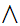
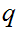 is a Boolean expression, whose truth table is
is a Boolean expression, whose truth table is 
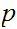 and
and
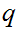 are Boolean expressions, then
are Boolean expressions, then
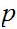
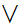
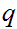 is a Boolean expression, whose truth table is
is a Boolean expression, whose truth table is 
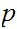 is a Boolean expressions, then
is a Boolean expressions, then
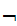
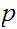 is a Boolean expression, whose truth table is
is a Boolean expression, whose truth table is