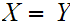
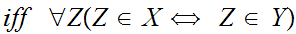 .
.
We will want to know how to do is how to construct sets. Unfortunately, as was discovered about 100 years ago, if you are not careful you get into trouble.
Axiom 1: Two sets are the same if and only if (write "iff") they have the same members.Symbolically,
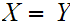
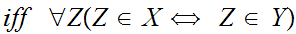 .
.
Axiom 2: Let
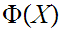 be
a proposition about mathematical objects then
be
a proposition about mathematical objects then
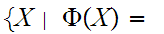 true
true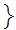 is
a set.
is
a set.
This sort of works! Try it. Look at the definitions of
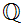 and
the open unit interval
and
the open unit interval
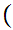 0,1
0,1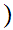 on
Page 0.
on
Page 0.
Here is more interesting example. Let
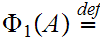
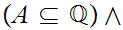
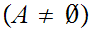
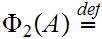
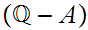
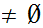
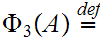
 x
x
 x
x 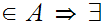 y
y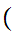 y
y 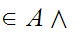 x
x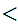 y
y
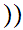
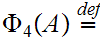
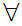 x
x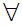 y
y
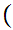 x
x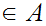
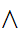 y
y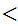 x
x
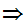 y
y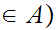
Let
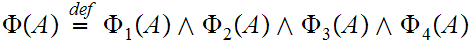
Then
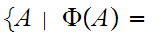 true
true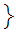 is the set of Dedekind cuts.
is the set of Dedekind cuts.
Let
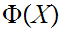 be
the proposition
"
be
the proposition
"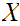 is
a set that does not contain itself as a member." That is,
is
a set that does not contain itself as a member." That is,
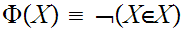 ,which
can be written
,which
can be written
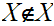 .
For almost any set that one thinks of
.
For almost any set that one thinks of
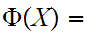 true.
The set
true.
The set
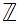 ,
of integers is not an integer. However, by the
Tentative Definition above, the set
of all sets is a set so it is a member of itself.
,
of integers is not an integer. However, by the
Tentative Definition above, the set
of all sets is a set so it is a member of itself.
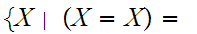 true
true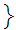
Now consider the set
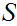 of
all sets that do not contain themselves as a member, that is
of
all sets that do not contain themselves as a member, that is
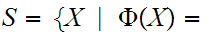 true
true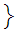 .
The question is
.
The question is
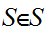 ?
Of course, as in the case of the barber , if
?
Of course, as in the case of the barber , if
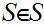 then
then
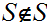 and
if
and
if
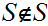 then
then
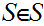 .
.
In point of fact, in order to do mathematics we do want to be able to work with some version of 2. In particular, the "collection" of mathematical objects satisfying a particular list of axioms. For example, in this course we want to talk about "metric spaces" and we will need to do this in a way that avoids Russell's Paradox. As a first step in the next section we take a very brief look at Axiomatic Set Theory .