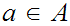 ,
we will use the notation,
,
we will use the notation,
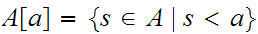
 for
the segment of
for
the segment of
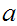 in
in
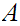 .
(rather than
.
(rather than
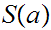 )
)
On this Page we assume all Sets are ordered.
11.1 Segments and "Ideal Cuts":
For
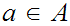 ,
we will use the notation,
,
we will use the notation,
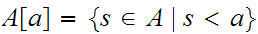
 for
the segment of
for
the segment of
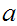 in
in
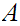 .
(rather than
.
(rather than
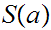 )
)
The text book defines a closely related notion of an Ideal, a
subset
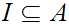 ,
having the property that
,
having the property that
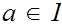 and
and
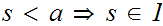 .
I will refer to an Ideal as an Ideal Cut (Think of Dedekind
Cut ) because
.
I will refer to an Ideal as an Ideal Cut (Think of Dedekind
Cut ) because
For any subset
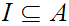 ,
is an Ideal Cut if and only if
,
is an Ideal Cut if and only if
 for every
for every
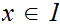 and
and
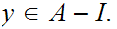
Hence if
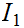 and
and
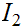 are
Ideal Cuts then
are
Ideal Cuts then
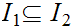 or
or
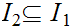 .
.
Also, if
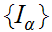 is a Set of Ideal Cuts, then so is
is a Set of Ideal Cuts, then so is
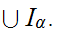
For any
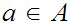 ,
,
![$\QTR{Large}{A[a]}$](graphics/ordered__21.png) is an Ideal Cut. More generally, any subset
is an Ideal Cut. More generally, any subset
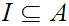 ,
is an Ideal Cut if for some subset
,
is an Ideal Cut if for some subset
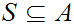 ,
,
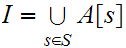
We also have
Let
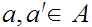 .
Show
.
Show
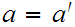
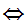
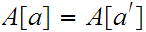
Let
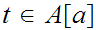 , show that
, show that
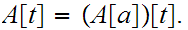 where the right side reads "The segment of
where the right side reads "The segment of
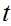 in
in
![$\QTR{Large}{A[a]}$](graphics/ordered__32.png) .
.
Proofs:
Verify for yourself:
Exercise due March 16;
If
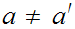 then
then
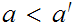 or
or
 .
If
.
If
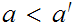 then
then
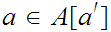 but by definition
but by definition
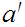
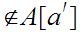 . If
. If
 ....
....
In general, for
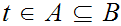 we have
we have
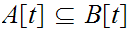 . What we need to show is that if
. What we need to show is that if
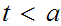 then
then
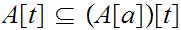 .
.
But
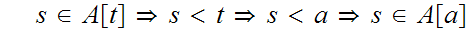
and
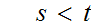 and
and
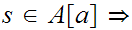
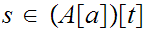
-----------------------------------------------------------------------------------------
11.2 Order morphisms :
A map
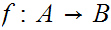 is said to be an order morphism if for all
is said to be an order morphism if for all
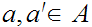 ,
,
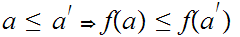 .
Unless there is a possibility of confusion we will use the symbol
.
Unless there is a possibility of confusion we will use the symbol
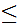 ambiguously.
ambiguously.
Let
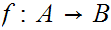 be a one to one order morphism then for all
be a one to one order morphism then for all
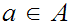
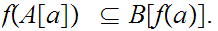
Let
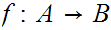 is said to an onto order morphism then for all
is said to an onto order morphism then for all
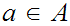
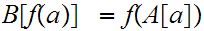 or
or
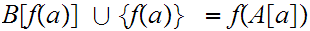
The Segment Mapping Formula - Let
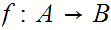 be
an order isomorphism (one to one, onto, and order preserving)
then for all
be
an order isomorphism (one to one, onto, and order preserving)
then for all
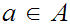 ,
,
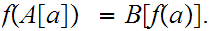
Proofs:
This amounts to observing that
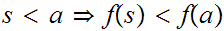 since
since
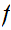 is
one to one.
is
one to one.
First note that
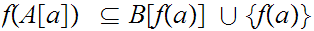 since
since
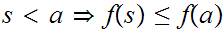
(It may the the case that
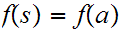 )
)
Next, let
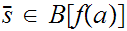 ,
in particular let
,
in particular let
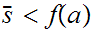 since
since
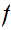 is
onto let
is
onto let
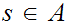 such that
such that
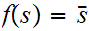
If
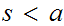 then
then
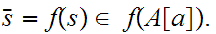 But
we cannot have
But
we cannot have
 since then
since then
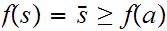 contradicting the choice of
contradicting the choice of
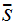 .
.
Hence
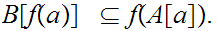
Follows from 1. and 2.