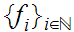 be a sequence of continuous functions for a metric space
be a sequence of continuous functions for a metric space
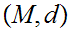 to a metric space
to a metric space
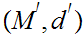 . The sequence is said to converge uniformly to
. The sequence is said to converge uniformly to
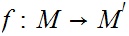 if
for any
if
for any
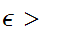 0
, there is a n such that
0
, there is a n such that
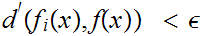 for all
for all
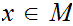 and i
and i
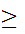 n
.
n
.
We outline a second proof that every Metric Space can be Isometrically Embedded in a Complete Metric Space. Much of the material on this Page is taken directly from section 5.1 of the text.
Let
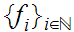 be a sequence of continuous functions for a metric space
be a sequence of continuous functions for a metric space
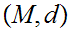 to a metric space
to a metric space
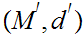 . The sequence is said to converge uniformly to
. The sequence is said to converge uniformly to
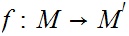 if
for any
if
for any
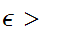 0
, there is a n such that
0
, there is a n such that
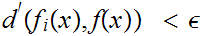 for all
for all
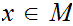 and i
and i
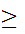 n
.
n
.
We write
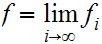 .
.
In the setting of 25.1,
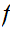 is continuous. That is the limit of a uniformly convergent sequence of
continuous functions is continuous.
is continuous. That is the limit of a uniformly convergent sequence of
continuous functions is continuous.
Proof:
We need to prove the continuity of
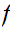 at each point
at each point
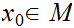 . Given
. Given
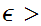 0
, Choose n such that
0
, Choose n such that
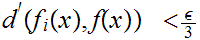 for all
for all
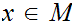 and i
and i
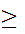 n.
Next choose
n.
Next choose
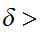 0,
such that for
0,
such that for
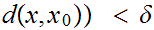 we have
we have
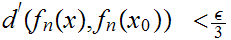
then for
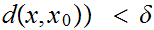
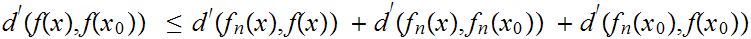
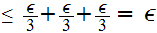
The following example shows that something like uniform convergence is necessary. seen

Let
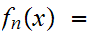 0
for
0
for
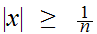
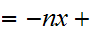 1
for
1
for
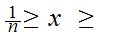 0
0
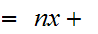 1
for
-
1
for
-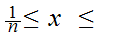 0
0
and
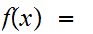 0
for
0
for
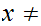 0
0
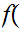 0
0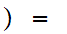 1
1
note that pointwise
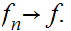
---------------------------------------------------------------------------------------------------------
The text discusses the following material in a more generalitly.
Given a Metric Space
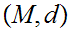 we let
we let
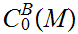 be the set of bounded real valued continuous functions on
be the set of bounded real valued continuous functions on
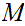 .
For
.
For
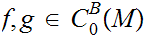 , define
, define
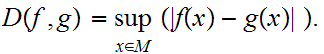
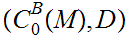 is a complete Metric Space.
is a complete Metric Space.
Proof:
A Good Review Exercise.
--------------------------------------------------------------------------------
Solution:
The essence of the proof is that definition allows you to work point by point.
To show
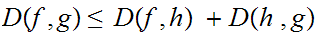 just
note that
just
note that
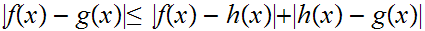 for every
for every
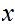 .
Hence
.
Hence
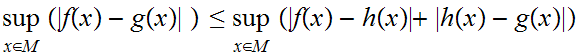
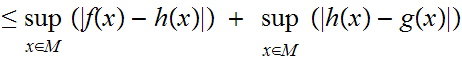
That is comple is even more straight forward. The definition tells us that a
"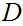 " Cauchy sequence is a Cauchy sequence for each
" Cauchy sequence is a Cauchy sequence for each
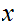 and that for any
and that for any
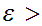 0
the same n works for all
0
the same n works for all
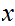 .
.
------------------------------------------------------------------------------------
There is an isometric embedding
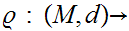
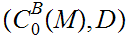 .
.
Proof:
Fix
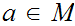 and
for all
and
for all
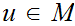 define
define
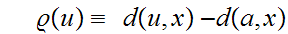
we need to verify that
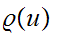 is
continuous.
is
continuous.
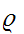 is
an isometric embedding.
is
an isometric embedding.
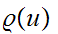 is
bounded.
is
bounded.
Proof:
Proving 2. first, suppose
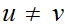 ,
then
,
then
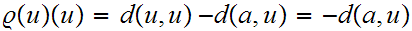
and
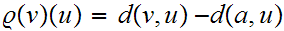
hence
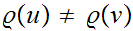
Moreover,
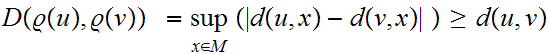 ,
choose
,
choose
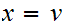
but by the 17.1.4 form of the triangle inequality, for
all
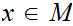 ,
,
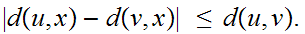
Note that 3. follows from the same inequality with
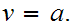
To prove 1. it suffices to check that for all
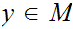 ,
,
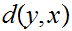 is continuous in
is continuous in
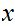 .
.
A Good Review Exercise.
--------------------------------------------------------------------------------
Solution:
To stress that
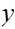 is fixed we will write
is fixed we will write
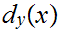 for
for
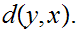 We need to show that for any
We need to show that for any
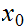 and
for any
and
for any
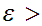 0
we can find a
0
we can find a
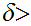 0
such that
0
such that
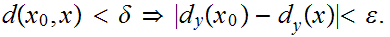
but
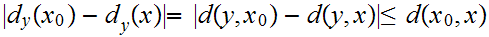
so choose
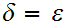 .
.