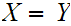
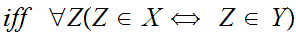 .
.
A Brief Introduction to Set Theory with Classes
(Godel-Bernays "GB")
For reference here, again, is pre-Russel's paradox Set Theory.
Axiom 1: Two sets are the same if and only if (write "iff") they have the same members.Symbolically,
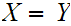
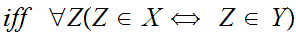 .
.
Axiom 2: Let
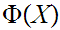 be
a proposition about mathematical objects then
be
a proposition about mathematical objects then
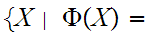 true
true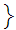 is
a Class.
is
a Class.
15.1 Terms and Relations in GB:
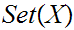 - read
"
- read
"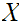 is a Set"
is a Set"
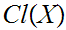 - read "
- read "
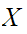 is
a Class"
is
a Class"
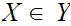 -
read "
-
read "
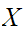 is
a member of
is
a member of
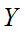 "
"
15.2 Some Axioms:
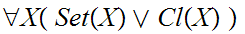 -
Everything is either a Set or a Class.
-
Everything is either a Set or a Class.
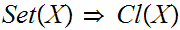 - Every Set is a Class.
- Every Set is a Class.
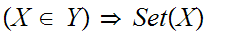 -
Every member of a Set or a Class is a Set.
-
Every member of a Set or a Class is a Set.
Let
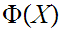 be
a proposition about mathematical objects
then
be
a proposition about mathematical objects
then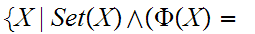 true
true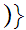 is
a Class.
is
a Class.
Restated:
Let
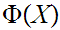 be
a proposition about mathematical objects then
be
a proposition about mathematical objects then
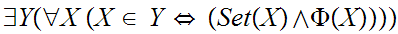
other ZF- type axioms.
15.3 Russel's paradox revisited:
Rewriting 4.
with 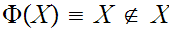 , the Russel example now reads. The exists a Class
, the Russel example now reads. The exists a Class
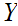 consisting of all Sets that do not contain themselves as members.
consisting of all Sets that do not contain themselves as members.
One asks is
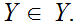
If
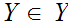 then
then
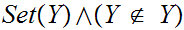 a contadiction.
a contadiction.
If
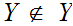 then
then
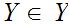 if and only if
if and only if
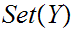 .
Hence if
.
Hence if
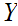 is
a Class but not a Set we do not have a contradiction. "The Barber does not
live on the island."
is
a Class but not a Set we do not have a contradiction. "The Barber does not
live on the island."
A CONSTRUCTIVE VERSION OF CANTOR'S THEOREM
Classical Set Theory:
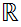 is uncountable .
is uncountable .
Constructive Set Theory: Let
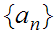 be a sequence of real numbers. let
be a sequence of real numbers. let
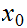 and
and
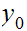 be real numbers with
be real numbers with
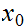
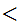
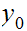 .
Then there exists a real number
.
Then there exists a real number
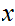 such that
such that
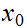
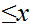
 and
and
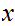
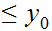
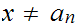 for all
for all
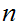 .
.
15.4 Definitions:
A real number
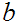 is called a constructive supremum, or constructive
least upper bound, of
is called a constructive supremum, or constructive
least upper bound, of
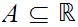 if it is an upper bound for
if it is an upper bound for
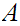 and if for each
and if for each
 there exists
there exists
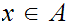 with
with
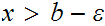 .
We write
.
We write
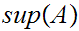
A real number
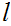 is called a contructive infimum, or constructive greatest lower bound, of A if
it is a lower bound for
is called a contructive infimum, or constructive greatest lower bound, of A if
it is a lower bound for
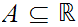 and if for each each
and if for each each
 there exists
there exists
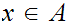 with
with
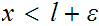 .
We write
.
We write
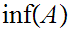
15.4 Theorem(Contructive lub). Let A be a nonempty set
of real numbers that is bounded above. Then
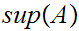 exists if and only if for all
exists if and only if for all
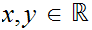 with
with
 ,
either
,
either
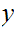 is an upper bound for
is an upper bound for
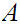 or there exists
or there exists
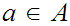 with
with
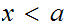 .
.